Complete probability formula
A relationship enabling one to calculate the unconditional probability of an event via its conditional probabilities with respect to events forming a complete set of alternatives.
More precisely, let  be a probability space, and let
be a probability space, and let  be events for which
be events for which  for
for  ,
,  ,
,
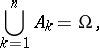 |
and  for all
for all  . Then one has the complete probability formula:
. Then one has the complete probability formula:
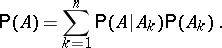 |
The complete probability formula also holds when the number of events 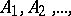 is infinite.
is infinite.
The complete probability formula holds for mathematical expectations. Let  ,
, 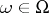 , be a random variable on
, be a random variable on 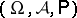 , let
, let 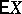 be its mathematical expectation and
be its mathematical expectation and  the conditional mathematical expectations with respect to events
the conditional mathematical expectations with respect to events 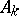 which form a complete set of alternatives. Then
which form a complete set of alternatives. Then
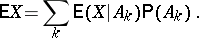 |
Comments
A complete set of alternatives is also called a partition of the sample space. A collection of events 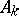 forms a partition if the events are disjoint, have positive probability and if their union is the sample space.
forms a partition if the events are disjoint, have positive probability and if their union is the sample space.
Complete probability formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_probability_formula&oldid=15372