Complete measure
From Encyclopedia of Mathematics
A measure  on a
on a  -algebra
-algebra  for which
for which 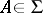 and
and  imply
imply  for every
for every  . Here
. Here  is the total variation of
is the total variation of  (
( for a positive measure).
for a positive measure).
Comments
Complete measures arise as follows (cf. [a1]). Let  be a set,
be a set,  a
a 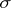 -algebra of subsets of it and
-algebra of subsets of it and 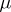 a positive measure on
a positive measure on  . It may happen that some set
. It may happen that some set  with
with  has a subset
has a subset 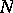 not belonging to
not belonging to  . It is natural, then, to define the measure
. It is natural, then, to define the measure 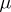 on such a set
on such a set  as
as  .
.
In general, let 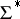 be the collection of all sets
be the collection of all sets 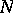 for which there exists sets
for which there exists sets 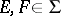 such that
such that  ,
, 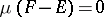 . In this situation, define
. In this situation, define  . Then
. Then 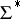 is a
is a 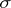 -algebra and
-algebra and 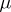 becomes a complete measure on it (this process is called completion).
becomes a complete measure on it (this process is called completion).  is then called a complete measure space.
is then called a complete measure space.
References
| [a1] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1974) pp. 24 |
| [a2] | E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) |
How to Cite This Entry:
Complete measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_measure&oldid=16648
Complete measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_measure&oldid=16648
This article was adapted from an original article by A.P. Terekhin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article