Complete group
From Encyclopedia of Mathematics
A group 
whose centre (cf. Centre of a group) is trivial (that is, 
is a so-called group without centre) and for which all automorphisms are inner (see Inner automorphism). The automorphism group of a complete group 
is isomorphic to 
itself (the term "complete" is related to this property). Examples of complete groups are the symmetric groups 
when 
(cf. Symmetric group). If a group 
contains a normal subgroup which is complete, then 
decomposes into a direct product 
of a subgroup 
and its centralizer in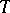 
.
References
| [1] | M.I. Kargapolov, Yu.I. Merzlyakov, "Fundamentals of group theory" , Moscow (1982) (In Russian) |
| [2] | M. Hall jr., "Group theory" , Chelsea (1976) |
How to Cite This Entry:
Complete group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_group&oldid=15667
Complete group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_group&oldid=15667
This article was adapted from an original article by N.N. Vil'yams (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article