Complete Dedekind lattice
From Encyclopedia of Mathematics
A complete lattice such that the identity
 |
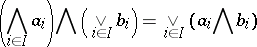is valid for any of its elements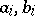 
, 
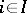, for which 
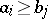if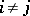 
. Any complete Dedekind lattice is a modular lattice. If a universal algebra has commuting congruences, then its congruence lattice is a complete Dedekind lattice [1].
References
| [1] | Ph. Dwinger, "Some theorems on universal algebras III" Indag. Math. , 20 (1958) pp. 70–76 |
Comments
The term "Dedekind lattice" is seldom used in the English language literature, instead one uses modular lattice (cf. [a1]). However, a complete modular lattice is a complete lattice satisfying the (finite) modular law. The notion defined in the article above has no established name; it could be called a completely modular lattice.
References
| [a1] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
How to Cite This Entry:
Complete Dedekind lattice. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_Dedekind_lattice&oldid=17947
Complete Dedekind lattice. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_Dedekind_lattice&oldid=17947
This article was adapted from an original article by O.A. Ivanova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article