Commutation and anti-commutation relationships, representation of
representation of commutation and anti-commutation relations
A linear weakly-continuous mapping 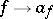 ,
, 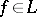 , from a pre-Hilbert space
, from a pre-Hilbert space 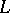 into a set of operators acting in some Hilbert space
into a set of operators acting in some Hilbert space 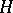 such that either the commutation relations
such that either the commutation relations
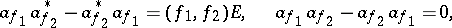 | (1) |
or the anti-commutation relations
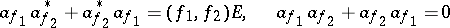 | (2) |
hold, where 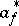 ,
, 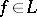 , is the adjoint of the operator
, is the adjoint of the operator 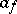 in
in 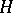 ,
, 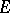 is the identity operator in
is the identity operator in 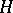 and
and 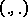 is the scalar product in
is the scalar product in 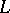 .
.
In the case when 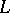 is finite-dimensional, all irreducible representations both of relation (1) and of (2) are unitarily equivalent. In the case of an infinite-dimensional space there are infinitely many distinct (not unitarily equivalent) irreducible representations of (1) and (2); for complete separable
is finite-dimensional, all irreducible representations both of relation (1) and of (2) are unitarily equivalent. In the case of an infinite-dimensional space there are infinitely many distinct (not unitarily equivalent) irreducible representations of (1) and (2); for complete separable  they are described in [2]–[5].
they are described in [2]–[5].
Operators 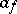 ,
, 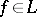 , satisfying (1) and (2) form the basis of the so-called second quantization formalism (where
, satisfying (1) and (2) form the basis of the so-called second quantization formalism (where 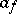 is usually called the annihilation operator of a particle in state
is usually called the annihilation operator of a particle in state 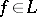 and
and 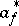 is the creation operator of this particle), often used in the study of quantum physical systems with a large number of degrees of freedom. However in second quantization one uses mainly the so-called Fock [Fok] representation of the commutation and anti-commutation relations; these are irreducible representations with as index space
is the creation operator of this particle), often used in the study of quantum physical systems with a large number of degrees of freedom. However in second quantization one uses mainly the so-called Fock [Fok] representation of the commutation and anti-commutation relations; these are irreducible representations with as index space 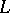 a separable Hilbert space, while in the space
a separable Hilbert space, while in the space 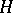 there exists a so-called vacuum vector that is annihilated by all operators
there exists a so-called vacuum vector that is annihilated by all operators 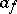 ,
, 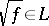 .
.
References
| [1] | F.A. Berezin, "The method of second quantization" , Acad. Press (1966) (Translated from Russian) (Revised (augmented) second edition: Kluwer, 1989) |
| [2] | I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , 4 , Acad. Press (1968) (Translated from Russian) |
| [3] | V.Ya. Golodets, "A description of the representation of anticommutation relations" Uspekhi Mat. Nauk , 24 : 4 (148) (1969) pp. 3–64 (In Russian) |
| [4a] | L. Gårding, A. Wightman, "Representations of the anticommutation relations" Proc. Nat. Acad. Sci. USA , 40 : 7 (1954) pp. 617–621 |
| [4b] | L. Gårding, A. Wightman, "Representations of the commutation relations" Proc. Nat. Acad. Sci. USA , 40 : 7 (1954) pp. 622–626 |
| [5] | I.E. Segal, "Distributions in Hilbert space and canonical systems of operators" Trans. Amer. Math. Soc. , 88 : 1 (1958) pp. 12–41 |
Comments
In Western literature the relations in question are often called canonical commutation and anti-commutation relations, and one uses the abbreviation CCR and CAR to denote them.
Two standard ways to write the CCR are (in the case of one degree of freedom)
 |
(where 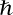 is Planck's constant, often taken equal to 1 in theoretical and mathematical considerations; the Heisenberg commutation relations) and
is Planck's constant, often taken equal to 1 in theoretical and mathematical considerations; the Heisenberg commutation relations) and
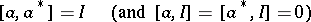 |
where  is the annihilation operator and
is the annihilation operator and 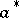 , its conjugate, is the creation operator. The relation between the two is exceedingly simple, viz.
, its conjugate, is the creation operator. The relation between the two is exceedingly simple, viz.
 |
The result that for finite-dimensional 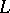 all (suitable) irreducible representations of the CCR are unitarily equivalent is the celebrated Stone–von Neumann theorem (also known as the von Neumann theorem, the von Neumann uniqueness theorem or the Stone–von Neumann uniqueness theorem). It only holds under suitable additional regularity assumptions, such as integrability of the representation involved to a representation of the associated group.
all (suitable) irreducible representations of the CCR are unitarily equivalent is the celebrated Stone–von Neumann theorem (also known as the von Neumann theorem, the von Neumann uniqueness theorem or the Stone–von Neumann uniqueness theorem). It only holds under suitable additional regularity assumptions, such as integrability of the representation involved to a representation of the associated group.
Thus, more precisely, consider the question of representing the relation 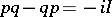 by means of operators on a Hilbert space (or, more generaly,
by means of operators on a Hilbert space (or, more generaly, 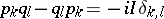 ,
, 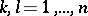 ). Abstractly these relations define an
). Abstractly these relations define an 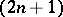 -dimensional Lie algebra over
-dimensional Lie algebra over 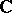 with basis
with basis  ,
, 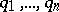 ,
, 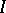 , called the Heisenberg Lie algebra or CCR algebra.
, called the Heisenberg Lie algebra or CCR algebra.
One particular representation of these relations is the Schrödinger representation, given by 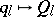 ,
, 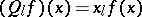 (where
(where  is short for
is short for 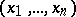 ) and
) and 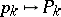 ,
, 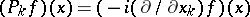 . This particular representation is integrable to a unitary representation with (in the case
. This particular representation is integrable to a unitary representation with (in the case 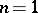 )
) 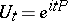 given by
given by 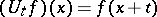 and
and 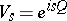 given by
given by 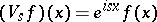 . The integrated unitary operators
. The integrated unitary operators 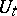 and
and 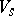 satisfy the Weyl commutation relations
satisfy the Weyl commutation relations
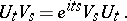 | (*) |
Define a Schrödinger couple to be a pair 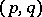 of self-adjoint operators on a countably infinite-dimensional Hilbert space such that
of self-adjoint operators on a countably infinite-dimensional Hilbert space such that 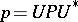 ,
, 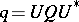 for some unitary operator
for some unitary operator 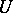 . Then one form of the von Neumann uniqueness theorem says that if
. Then one form of the von Neumann uniqueness theorem says that if 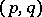 is a pair of self-adjoint operators on a Hilbert space such that the unitary groups
is a pair of self-adjoint operators on a Hilbert space such that the unitary groups 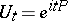 and
and 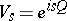 satisfy the Weyl commutation relations (*), then
satisfy the Weyl commutation relations (*), then 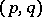 is a Schrödinger couple or a direct sum of such couples.
is a Schrödinger couple or a direct sum of such couples.
There are other, weaker, assumptions which guarantee uniqueness, such as the following one due to B. Rellich and J. Dixmier. Let 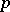 and
and 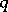 be closed symmetric operators on a Hilbert space with domains of definition
be closed symmetric operators on a Hilbert space with domains of definition 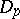 and
and 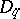 , respectively, such that
, respectively, such that 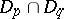 is dense. Suppose, moreover, that there exists a linear set
is dense. Suppose, moreover, that there exists a linear set  in
in 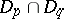 that is dense and such that
that is dense and such that 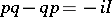 on
on  and
and 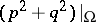 is essentially self-adjoint. Then
is essentially self-adjoint. Then 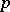 and
and  are self-adjoint and
are self-adjoint and 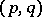 is a Schrödinger couple or a direct sum of such couples.
is a Schrödinger couple or a direct sum of such couples.
Thus, though it is true that if two unitary one-parameter groups 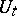 ,
, 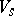 satisfy the Weyl commutation relation (*) then these infinitesimal generators satisfy the Heisenberg commutation relation
satisfy the Weyl commutation relation (*) then these infinitesimal generators satisfy the Heisenberg commutation relation  , the converse is not true. An example is given by the Hilbert space
, the converse is not true. An example is given by the Hilbert space 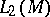 where
where 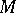 is the Riemann surface of
is the Riemann surface of 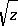 and
and 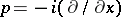 ,
, 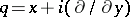 (cf. [a2], p. 275).
(cf. [a2], p. 275).
For a great deal more information concerning representations of the CCR cf., e.g., [a1], [a2], Sect. VIII.5, [a3], the classic [a4], and [a5], Chapt. 3.
For more details about the Fock representation of the CCR and CAR cf. Fock space
In the case of infinite degree of freedom (quantum field theory; infinite-dimensional 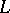 ) the Fock representation may very well be the wrong one to work with. In the case of interacting fields it is even typically the wrong one. This is an essential consequence of Haag's theorem (cf. [a5], Sect 3.c, and [a6] for a statement and discussions). Loosely speaking, Haag's theorem says that if a quantized field
) the Fock representation may very well be the wrong one to work with. In the case of interacting fields it is even typically the wrong one. This is an essential consequence of Haag's theorem (cf. [a5], Sect 3.c, and [a6] for a statement and discussions). Loosely speaking, Haag's theorem says that if a quantized field 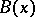 and its derivative at a given time may be mapped unitarily on a free field and its canonical conjugate, i.e. are "Fock" , then
and its derivative at a given time may be mapped unitarily on a free field and its canonical conjugate, i.e. are "Fock" , then 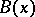 is itself a free field. Cf. Haag theorem for more details. Often Fock representations are used as a starting point and suitable non-Fock representations are constructed as weak limits (cf. [a7] for a specific example).
is itself a free field. Cf. Haag theorem for more details. Often Fock representations are used as a starting point and suitable non-Fock representations are constructed as weak limits (cf. [a7] for a specific example).
References
| [a1] | O. Bratteli, D.W. Robinson, "Operator algebras and quantum statistical mechanics" , II , Springer (1979) pp. Chapt. 5.2 |
| [a2] | M. Reed, B. Simon, "Methods of modern mathematical physics" , 1. Functional analysis , Acad. Press (1972) |
| [a3] | P.E.T. Jorgensen, R.T. Moore, "Operator commutator relations" , Reidel (1984) |
| [a4] | C.R. Putnam, "Commutation properties of Hilbert space operators and related topics" , Springer (1967) |
| [a5] | G.E. Emch, "Algebraic methods in statistical mechanics and quantum field theory" , Wiley (1972) |
| [a6] | L. Streit, "A generalization of Haag's theorem" Nuovo Cimento , 62A (1969) pp. 673–680 |
| [a7] | J.-P. Eckmann, "Representation of the 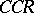 in the in the 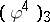 model: independence of the space cut-off" Comm. Math. Phys. , 25 (1972) pp. 1–61 model: independence of the space cut-off" Comm. Math. Phys. , 25 (1972) pp. 1–61 |
Commutation and anti-commutation relationships, representation of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Commutation_and_anti-commutation_relationships,_representation_of&oldid=17847