Cohomology ring
A ring the additive group of which is the graded cohomology group
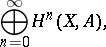 |
where  is a chain complex,
is a chain complex,  is a coefficient group and the multiplication is defined by the linear set of mappings
is a coefficient group and the multiplication is defined by the linear set of mappings
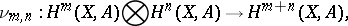 |
for all  , which are the inner cohomology multiplications (cup products). The cohomology ring turns out to be equipped with the structure of a graded ring.
, which are the inner cohomology multiplications (cup products). The cohomology ring turns out to be equipped with the structure of a graded ring.
For the existence of the mappings  it is enough to have a set of mappings
it is enough to have a set of mappings  satisfying certain additional properties, and a mapping
satisfying certain additional properties, and a mapping  , that is, a multiplication in the coefficient group
, that is, a multiplication in the coefficient group  (see [2]). The
(see [2]). The  induce mappings
induce mappings
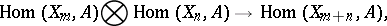 |
which in their turn induce mappings 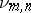 in cohomology.
in cohomology.
In particular, a ring structure is defined on the graded group  , where
, where  is a group and
is a group and 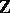 is the ring of integers with a trivial
is the ring of integers with a trivial  -action. The corresponding mappings
-action. The corresponding mappings  coincide with the
coincide with the 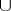 -product. This is an associative ring with identity, and for homogeneous elements
-product. This is an associative ring with identity, and for homogeneous elements 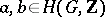 of degrees
of degrees  respectively,
respectively,  .
.
Analogously, the  -product defines a ring structure on the group
-product defines a ring structure on the group  , where
, where  is the
is the  -dimensional singular cohomology group of a topological space
-dimensional singular cohomology group of a topological space  with coefficients in
with coefficients in  .
.
References
| [1] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) |
| [2] | S. MacLane, "Homology" , Springer (1963) |
Comments
References
| [a1] | A. Dold, "Lectures on algebraic topology" , Springer (1972) pp. Chapt. VII |
Cohomology ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cohomology_ring&oldid=19247