Cohomological dimension
The cohomological dimension 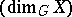 of a topological space
of a topological space 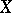 relative to the group of coefficients
relative to the group of coefficients 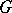 is the maximum integer
is the maximum integer 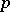 for which there exists closed subsets
for which there exists closed subsets 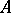 of
of 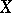 such that the cohomology groups
such that the cohomology groups  are non-zero. The homological dimension
are non-zero. The homological dimension 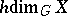 is similarly defined (cf. Homological dimension of a space). Finite Lebesgue dimension (covering dimension) is the same as
is similarly defined (cf. Homological dimension of a space). Finite Lebesgue dimension (covering dimension) is the same as 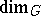 (or
(or 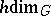 ) if
) if 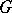 is the subgroup of the integers (or real numbers modulo 1). In Euclidean space
is the subgroup of the integers (or real numbers modulo 1). In Euclidean space 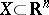 the equation
the equation 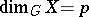 is equivalent to the property that
is equivalent to the property that 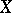 is locally linked by
is locally linked by  -dimensional cycles (with coefficients in
-dimensional cycles (with coefficients in 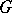 ). For paracompact spaces
). For paracompact spaces 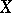 , the inequality
, the inequality 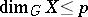 is equivalent to the existence of soft resolutions (cf. Soft sheaf and Resolution) for
is equivalent to the existence of soft resolutions (cf. Soft sheaf and Resolution) for 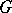 of length
of length 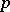 . Since soft sheaves are acyclic, in this way a connection is established with the general definition of dimension in homological algebra; for example, the injective (or projective) dimension of a module is
. Since soft sheaves are acyclic, in this way a connection is established with the general definition of dimension in homological algebra; for example, the injective (or projective) dimension of a module is 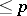 if it has an injective (or projective) resolution of length
if it has an injective (or projective) resolution of length 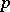 ; the global dimension of a ring is the maximum of the injective (or projective) dimensions of the modules over the ring and is the analogue of the Lebesgue dimension of
; the global dimension of a ring is the maximum of the injective (or projective) dimensions of the modules over the ring and is the analogue of the Lebesgue dimension of 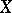 .
.
References
| [1] | P.S. Aleksandrov, Ann. of Math. (1929) pp. 101–187 , 30 |
| [2] | P.S. Aleksandrov, "Dimensionstheorie: Ein Beitrag zur Geometrie der abgeschlossenen Mengen" Math. Ann. , 106 (1932) pp. 161–238 |
| [3] | P.S. Aleksandrov, "An introduction to homological dimension theory and general combinatorial topology" , Moscow (1975) (In Russian) |
| [4] | A.E. [A.E. Kharlap] Harlap, "Local homology and cohomology, homology dimension and generalized manifolds" Math. USSR Sb. , 25 : 3 (1975) pp. 323–349 Mat. Sb. , 96 : 3 (1975) pp. 347–373 |
| [5] | V.I. Kuz'minov, "Homological dimension theory" Russian Math. Surveys , 29 : 5 (1968) pp. 1–45 Uspekhi Mat. Nauk , 23 : 5 (1968) pp. 3–49 |
| [6] | G.E. Bredon, "Sheaf theory" , McGraw-Hill (1967) |
| [7] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) |
E.G. Sklyarenko
The cohomological dimension of a scheme is the analogue of the notion of the cohomological dimension of a topological space for an algebraic variety or a scheme with a selected cohomology theory. Let 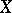 be an algebraic variety or a Noetherian scheme of dimension
be an algebraic variety or a Noetherian scheme of dimension  . The cohomological dimension of
. The cohomological dimension of 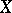 is defined to be the integer
is defined to be the integer 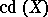 equal to the infimum of all those
equal to the infimum of all those 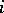 for which
for which 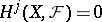 for all Abelian sheaves
for all Abelian sheaves 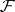 on the topological space
on the topological space 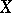 when
when 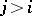 . The inequality
. The inequality
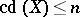 |
holds. The coherent cohomological dimension of the scheme 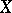 is the number
is the number 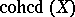 equal to the infimum of those
equal to the infimum of those 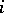 for which
for which 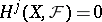 for all coherent algebraic sheaves
for all coherent algebraic sheaves 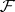 (cf. Coherent algebraic sheaf) on
(cf. Coherent algebraic sheaf) on 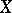 when
when 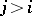 . By definition,
. By definition, 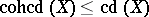 . By Serre's theorem,
. By Serre's theorem, 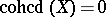 if and only if
if and only if 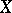 is an affine scheme. On the other hand, if
is an affine scheme. On the other hand, if 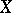 is an algebraic variety over a field
is an algebraic variety over a field 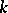 , then
, then 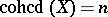 if and only if
if and only if 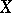 is proper over
is proper over 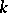 (Lichtenbaum's theorem, see [3]).
(Lichtenbaum's theorem, see [3]).
Let 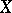 be a proper scheme over a field
be a proper scheme over a field 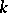 , let
, let 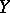 be a closed subscheme of
be a closed subscheme of 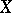 of codimension
of codimension  and let
and let 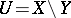 . Then the following statements hold ([2]–[4]).
. Then the following statements hold ([2]–[4]).
If 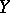 is the set-theoretic complete intersection of ample divisors on
is the set-theoretic complete intersection of ample divisors on 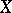 , then
, then
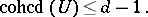 |
If 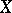 is a projective Cohen–Macaulay variety (for instance, a non-singular projective variety) and
is a projective Cohen–Macaulay variety (for instance, a non-singular projective variety) and 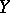 is zero-dimensional, then
is zero-dimensional, then 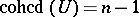 . The condition
. The condition 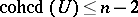 is equivalent to
is equivalent to 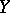 being connected. If
being connected. If 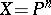 is a projective space and
is a projective space and 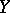 is connected and has dimension
is connected and has dimension 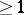 , then
, then
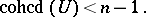 |
If 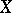 is a complex algebraic variety, then one can consider the cohomological dimension of the corresponding topological space
is a complex algebraic variety, then one can consider the cohomological dimension of the corresponding topological space 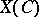 . In the general case when
. In the general case when 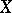 is a Noetherian scheme, the analogue of cohomological dimension is the notion of the étale cohomological dimension of the scheme
is a Noetherian scheme, the analogue of cohomological dimension is the notion of the étale cohomological dimension of the scheme 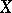 . More precisely, let
. More precisely, let 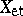 be the étale topology of the Grothendieck scheme
be the étale topology of the Grothendieck scheme 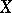 and let
and let 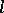 be a prime number. By the cohomological
be a prime number. By the cohomological 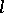 -dimension of the scheme
-dimension of the scheme 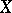 (or the étale cohomological dimension) one means the number
(or the étale cohomological dimension) one means the number 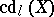 equal to the infimum of those
equal to the infimum of those 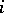 for which
for which 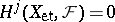 for all
for all 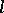 -torsion Abelian sheaves
-torsion Abelian sheaves 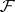 on
on 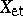 when
when 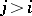 . If
. If 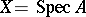 is an affine scheme, then
is an affine scheme, then 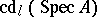 is also called the cohomological dimension of the ring
is also called the cohomological dimension of the ring  . In particular, if
. In particular, if 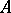 is a field, then the notion of
is a field, then the notion of  is the same as that of the cohomological dimension of a field as studied in the theory of Galois cohomology.
is the same as that of the cohomological dimension of a field as studied in the theory of Galois cohomology.
If 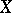 is an algebraic variety of dimension
is an algebraic variety of dimension  over a field
over a field 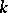 and if
and if 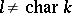 , then
, then 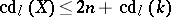 . In particular, if
. In particular, if 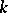 is a separably closed field, then
is a separably closed field, then 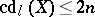 . If
. If 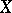 is an affine algebraic variety over the separably closed field
is an affine algebraic variety over the separably closed field 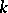 , then
, then 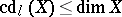 .
.
Let 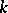 be a field of finite characteristic
be a field of finite characteristic 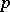 ; then for any Noetherian scheme
; then for any Noetherian scheme 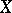 over
over 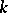 , the inequality
, the inequality
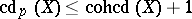 |
holds. In particular, for any Noetherian commutative ring 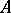 ,
,
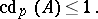 |
If 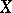 is a quasi-projective algebraic variety over the separably closed field
is a quasi-projective algebraic variety over the separably closed field 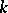 , then
, then 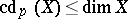 , where
, where  is the characteristic of
is the characteristic of 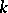 .
.
References
| [1] | A. Grothendieck, "Sur quelques points d'algèbre homologique" Tohôku Math. J. , 9 (1957) pp. 119–221 |
| [2] | R. Hartshorne, "Cohomological dimension of algebraic varieties" Ann. of Math. , 88 (1968) pp. 403–450 |
| [3] | R. Hartshorne, "Ample subvarieties of algebraic varieties" , Springer (1970) |
| [4] | R. Hartshorne, "Cohomology of non-complete algebraic varieties" Compositio Math. (1971) pp. 257–264 |
| [5] | M. Artin (ed.) A. Grothendieck (ed.) J.-L. Verdier (ed.) , Théorie des topos et cohomologie étale des schemas (SGA 4, vol. II, III) , Lect. notes in math. , 270; 305 , Springer (1972–1973) |
I.V. Dolgachev
Comments
References
| [a1] | B. Iversen, "Cohomology of sheaves" , Springer (1986) |
Cohomological dimension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cohomological_dimension&oldid=12764