Coherent algebraic sheaf
A coherent sheaf of modules on an algebraic variety or scheme. The structure sheaf of a Noetherian scheme and, in particular, of an algebraic variety is coherent.
Coherent algebraic sheaves are a convenient tool of investigating algebraic varieties. Intuitively, a coherent algebraic sheaf can be regarded as a continuous algebraic system of linear spaces on a variety (see Vector bundle on an algebraic variety) and arises in the consideration of linear and algebraic families of divisors, imbeddings of varieties in a projective space, differential forms, vector fields and automorphisms, deformations of varieties and subvarieties, in one word, in the linearization of all kinds of problems in algebraic geometry (see [3]). Here the results are stated in terms of the cohomology of coherent algebraic sheaves. The cohomology theory of coherent algebraic sheaves includes: a) finiteness theorems (in algebraic geometry), asserting the finiteness of the dimensions of the cohomology spaces  ,
,  , of a coherent sheaf
, of a coherent sheaf  on a complete variety
on a complete variety  ; b) the Riemann–Roch theorem, which calculates the Euler–Poincaré characteristic of a coherent algebraic sheaf; c) theorems of Serre type (see Affine scheme) or Kodaira vanishing theorems (cf. Kodaira theorem) (see [4], [5]); d) duality theorems (see Duality in algebraic geometry) relating the
; b) the Riemann–Roch theorem, which calculates the Euler–Poincaré characteristic of a coherent algebraic sheaf; c) theorems of Serre type (see Affine scheme) or Kodaira vanishing theorems (cf. Kodaira theorem) (see [4], [5]); d) duality theorems (see Duality in algebraic geometry) relating the 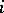 -dimensional and the
-dimensional and the  -dimensional cohomology spaces of sheaves on a smooth variety of dimension
-dimensional cohomology spaces of sheaves on a smooth variety of dimension  ; e) the Künneth formula, giving an expression for the homology spaces of certain sheaves on a product of varieties; f) comparison of theorems in algebraic geometry with other theorems on cohomology — analytic, formal, étale; and g) a theory of local cohomology, useful in the study of coherent algebraic sheaves on incomplete varieties. One of the most important of its applications relates to the Lefschetz theorem, which compares the properties of a variety and its hyperplane section.
; e) the Künneth formula, giving an expression for the homology spaces of certain sheaves on a product of varieties; f) comparison of theorems in algebraic geometry with other theorems on cohomology — analytic, formal, étale; and g) a theory of local cohomology, useful in the study of coherent algebraic sheaves on incomplete varieties. One of the most important of its applications relates to the Lefschetz theorem, which compares the properties of a variety and its hyperplane section.
Many results generalize to the case when the single variety  is replaced by a family of varieties, that is, to the case of a morphism
is replaced by a family of varieties, that is, to the case of a morphism  . In this case, the cohomology spaces are replaced by the sheaves
. In this case, the cohomology spaces are replaced by the sheaves 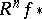 of the derived direct image functor
of the derived direct image functor 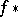 ; here an important role is played by the behaviour of these sheaves under a base change.
; here an important role is played by the behaviour of these sheaves under a base change.
See also Quasi-coherent sheaf; Cohomology with values in a sheaf.
References
| [1] | J.-P. Serre, "Faisceaux algébriques cohérents" Ann. of Math. , 61 (1955) pp. 197–278 MR0068874 Zbl 0067.16201 |
| [2] | A. Grothendieck, "Eléments de géometrie algébrique 3" Pub. Math. IHES , 11, 17 (1961) |
| [3] | D. Mumford, "Lectures on curves on an algebraic surface" , Princeton Univ. Press (1966) MR0209285 Zbl 0187.42701 |
| [4] | K. Kodaira, "On a differential-geometric method in the theory of stacks" Proc. Nat. Acad. Sci. USA , 39 (1953) pp. 1268–1273 MR66693 Zbl 0053.11701 |
| [5] | D. Mumford, "Pathologies III" Amer. J. Math. , 89 : 1 (1967) pp. 94–104 MR0217091 Zbl 0146.42403 |
| [6] | I.V. Dolgachev, "Abstract algebraic geometry" J. Soviet Math. , 2 (1974) pp. 264–303 Itogi Nauk. i Tekhn. Algebra. Geom. Topol. , 10 (1972) pp. 47–112 Zbl 1068.14059 |
Comments
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) MR0463157 Zbl 0367.14001 |
Coherent algebraic sheaf. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Coherent_algebraic_sheaf&oldid=14140