Cofibration
A triple  , where
, where 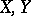 are topological spaces and
are topological spaces and  is an imbedding with the following property, known as the homotopy extension property with respect to polyhedra: For any polyhedron
is an imbedding with the following property, known as the homotopy extension property with respect to polyhedra: For any polyhedron 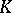 , any mapping
, any mapping  and any homotopy
and any homotopy
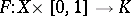 |
with
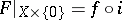 |
there exists a homotopy
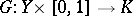 |
such that
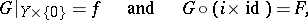 |
where
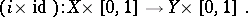 |
If this property holds with respect to any topological space, then the cofibration 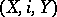 is known as a Borsuk pair (in fact, the term "cofibration" is sometimes also used in the sense of "Borsuk pair" ). The space
is known as a Borsuk pair (in fact, the term "cofibration" is sometimes also used in the sense of "Borsuk pair" ). The space 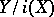 is called the cofibre of
is called the cofibre of 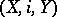 . The mapping cylinder construction converts any continuous mapping into a cofibration and makes it possible to construct a sequence
. The mapping cylinder construction converts any continuous mapping into a cofibration and makes it possible to construct a sequence
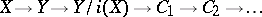 |
of topological spaces in which 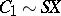 (
(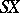 is the suspension of
is the suspension of 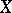 ) is the cofibre of the mapping
) is the cofibre of the mapping 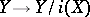 — being converted into a cofibration,
— being converted into a cofibration,  is the cofibre of the mapping
is the cofibre of the mapping  , etc. If
, etc. If  is a cofibration of pointed spaces, then for any pointed polyhedron
is a cofibration of pointed spaces, then for any pointed polyhedron  the induced sequence
the induced sequence
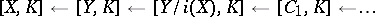 |
is an exact sequence of pointed sets; all terms of this sequence, from the fourth onward, are groups, and from the seventh onward — Abelian groups.
References
| [1] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) |
Comments
In Western literature a cofibration always means what is here called a Borsuk pair.
Cofibration. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cofibration&oldid=13585