Cofactor
From Encyclopedia of Mathematics
for a minor 
The number
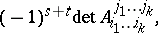 |
where  is a minor of order
is a minor of order  , with rows
, with rows  and columns
and columns  , of some square matrix
, of some square matrix  of order
of order  ;
;  is the determinant of the matrix of order
is the determinant of the matrix of order  obtained from
obtained from  by deletion of the rows and columns of
by deletion of the rows and columns of 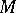 ;
; 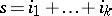 ,
,  . Laplace's theorem is valid: If any
. Laplace's theorem is valid: If any  rows are fixed in a determinant of order
rows are fixed in a determinant of order  , then the sum of the products of the minors of the
, then the sum of the products of the minors of the  -th order corresponding to the fixed rows by their cofactor is equal to the value of this determinant.
-th order corresponding to the fixed rows by their cofactor is equal to the value of this determinant.
Comments
This Laplace theorem is often referred to as Laplace's development of a determinant.
References
| [a1] | H.W. Turnball, "The theory of determinants, matrices, and invariants" , Dover, reprint (1980) |
How to Cite This Entry:
Cofactor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cofactor&oldid=15198
Cofactor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cofactor&oldid=15198
This article was adapted from an original article by V.N. Remeslennikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article