Coerciveness inequality
An inequality providing a lower bound for a certain bilinear form, or providing an upper bound for the norm of a solution of a certain elliptic boundary value problem, in terms of the coefficients of the elliptic equation and of the boundary data. Let
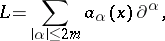 |
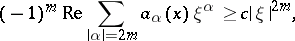 |
be a uniformly elliptic operator in a region 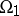 in
in 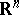 , with coefficients
, with coefficients 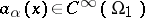 ; let
; let  be a subregion of
be a subregion of 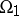 , and suppose that in some neighbourhood of the boundary
, and suppose that in some neighbourhood of the boundary 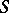 of
of  one has differential operators
one has differential operators 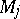 ,
, 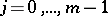 , of orders
, of orders 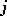 , the characteristics of which are not tangent to
, the characteristics of which are not tangent to 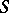 at any point of
at any point of 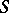 . Then, in some neighbourhood of
. Then, in some neighbourhood of 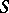 , there exist differential operators
, there exist differential operators 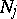 of orders
of orders 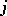 ,
, 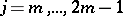 , such that
, such that
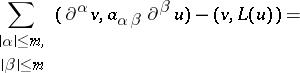 | (1) |
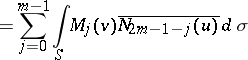 |
for all  in
in  . Here
. Here 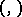 denotes the scalar product in
denotes the scalar product in 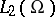 .
.
The form
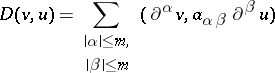 |
is called a coercive form on a space 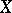 ,
, 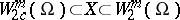 , if there exist constants
, if there exist constants 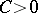 and
and 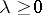 such that
such that
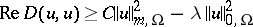 | (2) |
for all 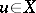 . Here
. Here 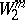 is the Sobolev space and
is the Sobolev space and 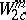 is the subspace of
is the subspace of 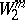 consisting of all elements with compact support, i.e. elements vanishing in a neighbourhood of the boundary of
consisting of all elements with compact support, i.e. elements vanishing in a neighbourhood of the boundary of  . Inequality (2) is a coerciveness inequality for the form
. Inequality (2) is a coerciveness inequality for the form 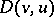 . If (2) remains valid with
. If (2) remains valid with 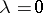 , then
, then 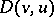 is said to be strongly coercive.
is said to be strongly coercive.
If a solution  of the equation
of the equation 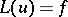 satisfies the conditions
satisfies the conditions 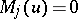 ,
, 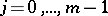 , on
, on 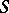 , then one has an inequality
, then one has an inequality
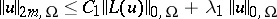 | (3) |
for some constants 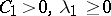 . If a solution
. If a solution  of the equation
of the equation 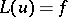 satisfies conditions
satisfies conditions 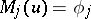 on
on 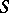 ,
,  , then instead of (3) one has the inequality
, then instead of (3) one has the inequality
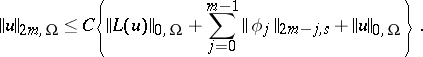 | (4) |
This inequality provides an estimate for the norm of the solution  of the equation
of the equation 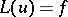 in the Sobolev space
in the Sobolev space 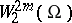 in terms of its norm in
in terms of its norm in 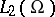 and of the norms of
and of the norms of 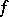 and
and 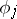 ,
, 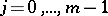 in the appropriate spaces. Inequality (4) is a coerciveness inequality for the boundary value problem for an elliptic equation.
in the appropriate spaces. Inequality (4) is a coerciveness inequality for the boundary value problem for an elliptic equation.
Using inequality (4) one obtains the more general inequality
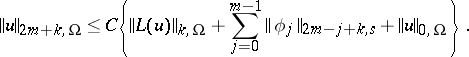 |
Coerciveness inequalities play an important role in the investigation of coercive boundary value problems and in proofs of the smoothness of solutions of elliptic equations; they are particularly important in analyticity proofs for solutions of analytic elliptic equations [2].
References
| [1] | S. Agmon, "Lectures on elliptic boundary value problems" , v. Nostrand (1965) |
| [2] | C.B. Morrey, L. Nirenberg, "On the analyticity of the solutions of linear elliptic systems of partial differential equations" Comm. Pure Appl. Math. , 10 : 2 (1957) pp. 271–290 |
Comments
Inequalities such as (3), (4), providing upper bounds for elliptic boundary value problems, are better known as boundary estimates for elliptic boundary value problems, instead of coerciveness inequalities. Lower bounds for bilinear forms are frequently encountered in the theory of variational inequalities (see also Variational equations). See also Coercive boundary value problem.
The functions 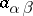 in (1) are obtained from the functions
in (1) are obtained from the functions 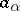 by integrating the expression
by integrating the expression 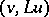 by parts. Clearly, the restriction
by parts. Clearly, the restriction 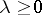 in (2) is inessential.
in (2) is inessential.
Coerciveness inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Coerciveness_inequality&oldid=18536