Difference between revisions of "Codimension"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 20: | Line 20: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , '''1''' , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French) {{MR|0354207}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Differentiable and analytic manifolds" , Addison-Wesley (1966) (Translated from French) {{MR|0205211}} {{MR|0205210}} {{ZBL|}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M. Golubitsky, "Stable mappings and their singularities" , Springer (1973) {{MR|0341518}} {{ZBL|0294.58004}} </TD></TR></table> |
Revision as of 16:56, 15 April 2012
The codimension (or quotient or factor dimension) of a subspace 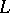 of a vector space
of a vector space 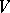 is the dimension of the quotient space
is the dimension of the quotient space 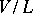 ; it is denoted by
; it is denoted by 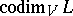 , or simply by
, or simply by 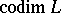 , and is equal to the dimension of the orthogonal complement of
, and is equal to the dimension of the orthogonal complement of 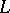 in
in 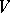 . One has
. One has
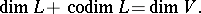 |
If 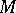 and
and 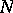 are two subspaces of
are two subspaces of 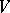 of finite codimension, then
of finite codimension, then 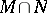 and
and 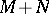 are also of finite codimension, and
are also of finite codimension, and
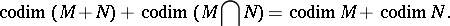 |
The codimension of a submanifold 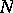 of a differentiable manifold
of a differentiable manifold 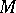 is the codimension of the tangent subspace
is the codimension of the tangent subspace 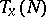 of the tangent space
of the tangent space 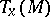 at
at 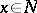 . If
. If 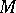 and
and 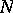 are finite-dimensional, then
are finite-dimensional, then
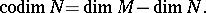 |
If 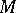 and
and 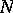 are differentiable manifolds, if
are differentiable manifolds, if 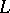 is a submanifold of
is a submanifold of 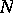 and if
and if 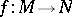 is a differentiable mapping transversal to
is a differentiable mapping transversal to 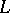 , then
, then
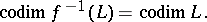 |
The codimension of an algebraic subvariety (or an analytic subspace) 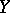 of an algebraic variety (analytic space)
of an algebraic variety (analytic space) 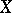 is the difference
is the difference
 |
References
| [1] | N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , 1 , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French) MR0354207 |
| [2] | N. Bourbaki, "Elements of mathematics. Differentiable and analytic manifolds" , Addison-Wesley (1966) (Translated from French) MR0205211 MR0205210 |
| [3] | M. Golubitsky, "Stable mappings and their singularities" , Springer (1973) MR0341518 Zbl 0294.58004 |
Comments
The codimension of a subspace 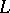 of a vector space
of a vector space 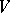 is equal to the dimension of any complement of
is equal to the dimension of any complement of 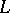 in
in 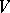 , since all complements have the same dimension (as the orthogonal complement).
, since all complements have the same dimension (as the orthogonal complement).
Codimension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Codimension&oldid=18855