Code with correction of deletions and insertions
code for correction of deletions and insertions
A code intended for the correction of errors of two types encountered in the transmission of information. By a deletion of a letter in a word 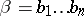 of length
of length  over some alphabet
over some alphabet 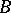 one means a transformation of
one means a transformation of 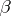 into a word
into a word 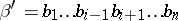 of length
of length 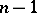 ,
, 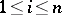 . The numbers
. The numbers 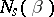 of words obtainable from
of words obtainable from 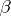 by deletion of
by deletion of  letters satisfies the following estimates
letters satisfies the following estimates
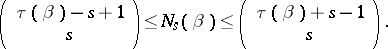 |
Here 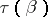 is the number of series of
is the number of series of 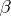 (by a series of a word
(by a series of a word 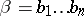 one means a word
one means a word 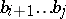 ,
, 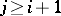 , such that 1)
, such that 1) 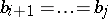 ; 2) if
; 2) if 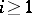 , then
, then 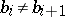 ; and 3) if
; and 3) if 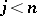 , then
, then 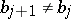 ). In particular,
). In particular, 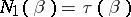 . By an insertion of a letter in a word
. By an insertion of a letter in a word 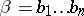 one means a transformation of
one means a transformation of 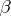 into a word
into a word 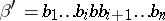 of length
of length 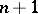 , where
, where 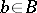 and
and 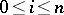 . The number of words obtainable from an arbitrary word
. The number of words obtainable from an arbitrary word 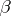 of length
of length  by the insertion of
by the insertion of  letters of an alphabet
letters of an alphabet 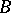 is equal to
is equal to
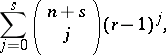 |
where  is the number of letters in
is the number of letters in 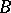 . A set
. A set 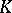 of words over the alphabet
of words over the alphabet 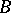 is called a code for correction of
is called a code for correction of  deletions (insertions, deletions or insertions) if no word in
deletions (insertions, deletions or insertions) if no word in 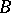 can be obtained from two distinct words of
can be obtained from two distinct words of  as the result of
as the result of  or fewer deletions (insertions, deletions or insertions) of letters in each of them. The function defined on the pairs
or fewer deletions (insertions, deletions or insertions) of letters in each of them. The function defined on the pairs 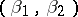 of words in
of words in 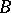 and equal to the minimum number of deletions and insertions of letters converting
and equal to the minimum number of deletions and insertions of letters converting 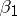 into
into 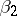 is a metric. A set
is a metric. A set 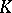 of words over the alphabet
of words over the alphabet 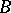 is a code for correction of
is a code for correction of  deletions (insertions, deletions or insertions) if and only if the distance between any two distinct words of
deletions (insertions, deletions or insertions) if and only if the distance between any two distinct words of 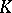 is greater than
is greater than  , so that the above three definitions of a code are equivalent. An example of a code for correction of one deletion or one insertion is the set of words
, so that the above three definitions of a code are equivalent. An example of a code for correction of one deletion or one insertion is the set of words 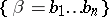 of length
of length  over the alphabet
over the alphabet 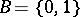 for which
for which 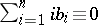 (
(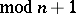 ). The number of words in this code is equal to
). The number of words in this code is equal to
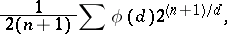 |
where the sum is taken over all odd divisors 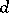 of
of 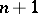 and
and 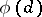 is the Euler function; it is asymptotically maximal as
is the Euler function; it is asymptotically maximal as 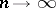 .
.
Code with correction of deletions and insertions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Code_with_correction_of_deletions_and_insertions&oldid=11397