Difference between revisions of "Code with correction of arithmetical errors"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | c0228501.png | ||
| + | $#A+1 = 96 n = 1 | ||
| + | $#C+1 = 96 : ~/encyclopedia/old_files/data/C022/C.0202850 Code with correction of arithmetical errors, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''code for correction of arithmetic errors, code that corrects arithmetic errors, arithmetic code'' | ''code for correction of arithmetic errors, code that corrects arithmetic errors, arithmetic code'' | ||
| − | A code intended for the control of the functioning of an adder. When adding numbers represented in the binary number system, a single slip in the functioning of the adder leads, as a rule, to a change in the result by some power of 2. In this connection, a (single) arithmetic error in the ring of integers | + | A code intended for the control of the functioning of an adder. When adding numbers represented in the binary number system, a single slip in the functioning of the adder leads, as a rule, to a change in the result by some power of 2. In this connection, a (single) arithmetic error in the ring of integers $ \mathbf Z $ |
| + | is defined as a transformation of a number $ N $ | ||
| + | to a number $ N ^ { \prime } = N \pm 2 ^ {i} $, | ||
| + | $ i = 0, 1 , . . . $. | ||
| + | The function $ \rho ( N _ {1} , N _ {2} ) $ | ||
| + | on $ \mathbf Z \times \mathbf Z $, | ||
| + | defined as the minimum number of arithmetic errors taking $ N _ {1} $ | ||
| + | to $ N _ {2} $, | ||
| + | is a metric. An arbitrary finite subset (a code) $ K \subset \mathbf Z $ | ||
| + | is characterized by its minimum distance | ||
| − | + | $$ | |
| + | \rho ( K) = \ | ||
| + | \min \rho ( N _ {1} , N _ {2} ), | ||
| + | $$ | ||
| − | where the minimum is taken over all distinct | + | where the minimum is taken over all distinct $ N _ {1} , N _ {2} \in K $. |
| + | The sets of $ t $ | ||
| + | or fewer arithmetic errors transform a number $ N $ | ||
| + | into a metric ball of radius $ t $ | ||
| + | and centre $ N $. | ||
| + | Therefore if the metric balls of radius $ t $ | ||
| + | described around any two numbers of a code do not intersect (that is, if the minimum distance of the code is greater than $ 2t $), | ||
| + | then the code is said to be a code that corrects $ t $ | ||
| + | arithmetic errors. If the metric ball of radius $ s $ | ||
| + | described around any number of the code contains no other numbers of the code (that is, if the minimum distance of the code is greater than $ s $), | ||
| + | then the code is called a code that detects $ s $ | ||
| + | arithmetic errors. The metric $ \rho $ | ||
| + | has the following alternative description: | ||
| − | + | $$ | |
| + | \rho ( N _ {1} , N _ {2} ) = \ | ||
| + | w ( N _ {1} - N _ {2} ), | ||
| + | $$ | ||
| − | where | + | where $ w ( N) $ |
| + | is the (arithmetic) weight of $ N $, | ||
| + | i.e. the smallest possible number of non-zero coefficients in the representations | ||
| − | + | $$ \tag{* } | |
| + | N = \sum _ {i = 0 } ^ { k } | ||
| + | N _ {i} 2 ^ {i} ,\ \ | ||
| + | N _ {i} = 0, \pm 1; \ \ | ||
| + | k = 0, 1 , . . . . | ||
| + | $$ | ||
| − | For each | + | For each $ N $ |
| + | there is a unique representation (*) on which $ N _ {k} \neq 0 $, | ||
| + | $ N _ {i} N _ {i + 1 } = 0 $, | ||
| + | $ i = 0 \dots k - 1 $, | ||
| + | and the number of non-zero coefficients in the representation is $ w ( N) $. | ||
| + | For example, $ 23 = 2 ^ {4} + 2 ^ {2} + 2 ^ {1} + 2 ^ {0} = 2 ^ {5} - 2 ^ {3} - 2 ^ {0} $ | ||
| + | and $ w ( 23) = 3 $. | ||
| + | Since $ \rho ( N _ {1} + N, N _ {2} + N) = \rho ( N _ {1} , N _ {2} ) $ | ||
| + | for any $ N _ {1} , N _ {2} , N \in \mathbf Z $, | ||
| + | one restricts attention to codes that do not contain negative numbers. By the length of a code $ K $ | ||
| + | one means the quantity $ [ \mathop{\rm log} _ {2} B ( K)] + 1 $, | ||
| + | where $ B ( K) $ | ||
| + | is the largest number of the code $ K $. | ||
| + | There corresponds to an arbitrary number $ B $ | ||
| + | of a code of length $ n $ | ||
| + | a unique word $ \beta ( B) = b _ {n - 1 } \dots b _ {0} $ | ||
| + | over the alphabet $ \{ 0, 1 \} $ | ||
| + | such that $ B = \sum _ {i = 0 } ^ {n - 1 } b _ {i} 2 ^ {i} $. | ||
| + | If the code $ K \subset \mathbf Z $ | ||
| + | corrects $ t $ | ||
| + | arithmetic errors, then the code $ \{ {\beta ( B) } : {B \in K } \} $ | ||
| + | corrects $ t $ | ||
| + | errors (of substitution type) by virtue of the fact that $ d ( \beta ( B _ {1} ), \beta ( B _ {2} )) \geq \rho ( B _ {1} , B _ {2} ) $, | ||
| + | where $ d ( \cdot , \cdot ) $ | ||
| + | is the Hamming metric (see [[Error-correcting code|Error-correcting code]]). In the study of problems of control of an adder one usually considers an encoding $ f: \{ 0 \dots M - 1 \} \rightarrow \mathbf Z $( | ||
| + | see [[Coding and decoding|Coding and decoding]]) such that $ f ( i + j) = f ( i) + f ( j) $ | ||
| + | for $ i + j < M $( | ||
| + | which is equivalent to $ f ( i) = A \cdot i $, | ||
| + | where $ A = f ( 1) $). | ||
| + | In this case, the coding operation consists in the multiplication of the number to be encoded by $ A $, | ||
| + | while the detection of errors in the functioning of the adder consists in verifying that the result of the addition is divisible by $ A $. | ||
| + | The code $ K _ {A,M} = \{ 0, A \dots A ( M - 1) \} $ | ||
| + | is called an $ AM $- | ||
| + | code. The minimum distance of an $ AM $- | ||
| + | code is the minimum of the $ w ( A \cdot i) $, | ||
| + | $ i = 1 \dots M - 1 $. | ||
| + | For example, the minimum distance of a $ 3M $- | ||
| + | code is equal to 2; the code detects single arithmetic errors and is often applied in computers (in the form of a control modulo 3). The best studied are (cyclic and negacyclic) $ AM $- | ||
| + | codes with $ M = ( 2 ^ {n} \pm 1)/A $; | ||
| + | they are characterized by the property that whenever the number $ B = \sum _ {i = 0 } ^ {n - 1 } b _ {i} 2 ^ {i} $, | ||
| + | $ b _ {i} = 0, 1 $, | ||
| + | belongs to the code, then so does the number $ B ^ { \prime } = \pm b _ {n - 1 } + \sum _ {i = 1 } ^ {n - 1 } b _ {i} 2 ^ {i} $. | ||
| + | Such codes, called $ ( n, A) $- | ||
| + | codes, can be conveniently regarded as subsets of the metric space $ \mathbf N _ {m} = \{ {0 \dots m - 1 } : {m = 2 ^ {n} \pm 1 } \} $, | ||
| + | with metric $ \rho _ {m} ( x, y) = w _ {m} ( x - y) = \min \{ w ( x - y), w ( x - y - m) \} $. | ||
| + | The minimum distances of an $ ( n, A) $- | ||
| + | code in the metrics $ \rho $ | ||
| + | and $ \rho _ {m} $ | ||
| + | are equal. To each $ ( n, A) $- | ||
| + | code there is associated the $ ( n, A ^ {*} ) $- | ||
| + | code where $ AA ^ {*} = m $; | ||
| + | it is called the dual code. If 2 or $ - 2 $ | ||
| + | are primitive roots modulo a prime number $ p $, | ||
| + | then the $ (( p - 1)/2, p) $- | ||
| + | code corrects single arithmetic errors and is perfect in the metric $ \rho _ {m} $, | ||
| + | that is, the metric balls of radius 1 described around the numbers of the code are not only pairwise disjoint but also fill out the whole of $ \mathbf N _ {m} $. | ||
| + | In the dual code, all distances between different numbers of the code are equal to $ \left ] ( p + 1)/6 \right [ $. | ||
| + | The results listed above for codes are analogues of results for binary linear cyclic error-correcting codes. Meanwhile, there are no known arithmetic analogues of B.C.H. (Bose–Chaudhury–Hocquenghem)-codes; nor are there any known upper bounds for the size of codes with given length and distance, analogous to the best bound for error-correcting codes. Codes correcting $ q $- | ||
| + | ary arithmetic errors $ ( q > 2) $ | ||
| + | possess even more characteristics (a $ q $- | ||
| + | ary arithmetical error is a transformation of a number $ N $ | ||
| + | to a number $ N ^ { \prime } = N \pm aq ^ {i} $, | ||
| + | $ a = 1 \dots q - 1 $; | ||
| + | $ i = 0, 1 , . . . $). | ||
| + | Interest in such codes has increased with the development of computing techniques. Thus, in contrast to error-correcting codes, there are no perfect $ AM $- | ||
| + | codes with $ q = 2 ^ {l} $( | ||
| + | $ l > 1 $) | ||
| + | that correct single $ q $- | ||
| + | ary arithmetic errors; for $ q = 6 $ | ||
| + | there are examples known of such codes. Existence conditions for perfect $ AM $- | ||
| + | codes are of a number-theoretic character and are connected with the study of reciprocity laws in number fields. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> Yu.G. Dadaev, "The theory of arithmetic codes" , Moscow (1981) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E. Weldon jr., "Error-correcting codes" , M.I.T. (1972)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J.L. Massey, O.N. Garcia, , ''Advances in information systems science'' , '''4''' , New York-London (1972) pp. 273–326</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> I.M. Boyarinov, G.A. Kabatyanskii, "Perfect single-error-correcting arithmetic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022850/c022850102.png" />-codes" ''Problemy Peredachi Informatsii'' , '''12''' : 1 (1976) pp. 16–23 (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> Yu.G. Dadaev, "The theory of arithmetic codes" , Moscow (1981) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E. Weldon jr., "Error-correcting codes" , M.I.T. (1972)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J.L. Massey, O.N. Garcia, , ''Advances in information systems science'' , '''4''' , New York-London (1972) pp. 273–326</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> I.M. Boyarinov, G.A. Kabatyanskii, "Perfect single-error-correcting arithmetic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022850/c022850102.png" />-codes" ''Problemy Peredachi Informatsii'' , '''12''' : 1 (1976) pp. 16–23 (In Russian)</TD></TR></table> | ||
Revision as of 17:45, 4 June 2020
code for correction of arithmetic errors, code that corrects arithmetic errors, arithmetic code
A code intended for the control of the functioning of an adder. When adding numbers represented in the binary number system, a single slip in the functioning of the adder leads, as a rule, to a change in the result by some power of 2. In this connection, a (single) arithmetic error in the ring of integers $ \mathbf Z $ is defined as a transformation of a number $ N $ to a number $ N ^ { \prime } = N \pm 2 ^ {i} $, $ i = 0, 1 , . . . $. The function $ \rho ( N _ {1} , N _ {2} ) $ on $ \mathbf Z \times \mathbf Z $, defined as the minimum number of arithmetic errors taking $ N _ {1} $ to $ N _ {2} $, is a metric. An arbitrary finite subset (a code) $ K \subset \mathbf Z $ is characterized by its minimum distance
$$ \rho ( K) = \ \min \rho ( N _ {1} , N _ {2} ), $$
where the minimum is taken over all distinct $ N _ {1} , N _ {2} \in K $. The sets of $ t $ or fewer arithmetic errors transform a number $ N $ into a metric ball of radius $ t $ and centre $ N $. Therefore if the metric balls of radius $ t $ described around any two numbers of a code do not intersect (that is, if the minimum distance of the code is greater than $ 2t $), then the code is said to be a code that corrects $ t $ arithmetic errors. If the metric ball of radius $ s $ described around any number of the code contains no other numbers of the code (that is, if the minimum distance of the code is greater than $ s $), then the code is called a code that detects $ s $ arithmetic errors. The metric $ \rho $ has the following alternative description:
$$ \rho ( N _ {1} , N _ {2} ) = \ w ( N _ {1} - N _ {2} ), $$
where $ w ( N) $ is the (arithmetic) weight of $ N $, i.e. the smallest possible number of non-zero coefficients in the representations
$$ \tag{* } N = \sum _ {i = 0 } ^ { k } N _ {i} 2 ^ {i} ,\ \ N _ {i} = 0, \pm 1; \ \ k = 0, 1 , . . . . $$
For each $ N $ there is a unique representation (*) on which $ N _ {k} \neq 0 $, $ N _ {i} N _ {i + 1 } = 0 $, $ i = 0 \dots k - 1 $, and the number of non-zero coefficients in the representation is $ w ( N) $. For example, $ 23 = 2 ^ {4} + 2 ^ {2} + 2 ^ {1} + 2 ^ {0} = 2 ^ {5} - 2 ^ {3} - 2 ^ {0} $ and $ w ( 23) = 3 $. Since $ \rho ( N _ {1} + N, N _ {2} + N) = \rho ( N _ {1} , N _ {2} ) $ for any $ N _ {1} , N _ {2} , N \in \mathbf Z $, one restricts attention to codes that do not contain negative numbers. By the length of a code $ K $ one means the quantity $ [ \mathop{\rm log} _ {2} B ( K)] + 1 $, where $ B ( K) $ is the largest number of the code $ K $. There corresponds to an arbitrary number $ B $ of a code of length $ n $ a unique word $ \beta ( B) = b _ {n - 1 } \dots b _ {0} $ over the alphabet $ \{ 0, 1 \} $ such that $ B = \sum _ {i = 0 } ^ {n - 1 } b _ {i} 2 ^ {i} $. If the code $ K \subset \mathbf Z $ corrects $ t $ arithmetic errors, then the code $ \{ {\beta ( B) } : {B \in K } \} $ corrects $ t $ errors (of substitution type) by virtue of the fact that $ d ( \beta ( B _ {1} ), \beta ( B _ {2} )) \geq \rho ( B _ {1} , B _ {2} ) $, where $ d ( \cdot , \cdot ) $ is the Hamming metric (see Error-correcting code). In the study of problems of control of an adder one usually considers an encoding $ f: \{ 0 \dots M - 1 \} \rightarrow \mathbf Z $( see Coding and decoding) such that $ f ( i + j) = f ( i) + f ( j) $ for $ i + j < M $( which is equivalent to $ f ( i) = A \cdot i $, where $ A = f ( 1) $). In this case, the coding operation consists in the multiplication of the number to be encoded by $ A $, while the detection of errors in the functioning of the adder consists in verifying that the result of the addition is divisible by $ A $. The code $ K _ {A,M} = \{ 0, A \dots A ( M - 1) \} $ is called an $ AM $- code. The minimum distance of an $ AM $- code is the minimum of the $ w ( A \cdot i) $, $ i = 1 \dots M - 1 $. For example, the minimum distance of a $ 3M $- code is equal to 2; the code detects single arithmetic errors and is often applied in computers (in the form of a control modulo 3). The best studied are (cyclic and negacyclic) $ AM $- codes with $ M = ( 2 ^ {n} \pm 1)/A $; they are characterized by the property that whenever the number $ B = \sum _ {i = 0 } ^ {n - 1 } b _ {i} 2 ^ {i} $, $ b _ {i} = 0, 1 $, belongs to the code, then so does the number $ B ^ { \prime } = \pm b _ {n - 1 } + \sum _ {i = 1 } ^ {n - 1 } b _ {i} 2 ^ {i} $. Such codes, called $ ( n, A) $- codes, can be conveniently regarded as subsets of the metric space $ \mathbf N _ {m} = \{ {0 \dots m - 1 } : {m = 2 ^ {n} \pm 1 } \} $, with metric $ \rho _ {m} ( x, y) = w _ {m} ( x - y) = \min \{ w ( x - y), w ( x - y - m) \} $. The minimum distances of an $ ( n, A) $- code in the metrics $ \rho $ and $ \rho _ {m} $ are equal. To each $ ( n, A) $- code there is associated the $ ( n, A ^ {*} ) $- code where $ AA ^ {*} = m $; it is called the dual code. If 2 or $ - 2 $ are primitive roots modulo a prime number $ p $, then the $ (( p - 1)/2, p) $- code corrects single arithmetic errors and is perfect in the metric $ \rho _ {m} $, that is, the metric balls of radius 1 described around the numbers of the code are not only pairwise disjoint but also fill out the whole of $ \mathbf N _ {m} $. In the dual code, all distances between different numbers of the code are equal to $ \left ] ( p + 1)/6 \right [ $. The results listed above for codes are analogues of results for binary linear cyclic error-correcting codes. Meanwhile, there are no known arithmetic analogues of B.C.H. (Bose–Chaudhury–Hocquenghem)-codes; nor are there any known upper bounds for the size of codes with given length and distance, analogous to the best bound for error-correcting codes. Codes correcting $ q $- ary arithmetic errors $ ( q > 2) $ possess even more characteristics (a $ q $- ary arithmetical error is a transformation of a number $ N $ to a number $ N ^ { \prime } = N \pm aq ^ {i} $, $ a = 1 \dots q - 1 $; $ i = 0, 1 , . . . $). Interest in such codes has increased with the development of computing techniques. Thus, in contrast to error-correcting codes, there are no perfect $ AM $- codes with $ q = 2 ^ {l} $( $ l > 1 $) that correct single $ q $- ary arithmetic errors; for $ q = 6 $ there are examples known of such codes. Existence conditions for perfect $ AM $- codes are of a number-theoretic character and are connected with the study of reciprocity laws in number fields.
References
| [1] | Yu.G. Dadaev, "The theory of arithmetic codes" , Moscow (1981) (In Russian) |
| [2] | E. Weldon jr., "Error-correcting codes" , M.I.T. (1972) |
| [3] | J.L. Massey, O.N. Garcia, , Advances in information systems science , 4 , New York-London (1972) pp. 273–326 |
| [4] | I.M. Boyarinov, G.A. Kabatyanskii, "Perfect single-error-correcting arithmetic 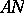 -codes" Problemy Peredachi Informatsii , 12 : 1 (1976) pp. 16–23 (In Russian) -codes" Problemy Peredachi Informatsii , 12 : 1 (1976) pp. 16–23 (In Russian) |
Code with correction of arithmetical errors. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Code_with_correction_of_arithmetical_errors&oldid=46377