Cochain
A homogeneous element of an Abelian cochain group 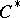 (or, in the general case, a module), i.e. a graded Abelian group equipped with an endomorphism
(or, in the general case, a module), i.e. a graded Abelian group equipped with an endomorphism 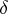 of degree
of degree 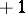 such that
such that 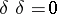 . The endomorphism
. The endomorphism 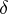 is called the coboundary mapping or the coboundary.
is called the coboundary mapping or the coboundary.
A cochain group 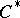 usually arises as a group
usually arises as a group 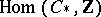 or
or  , where
, where 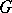 is an arbitrary Abelian group, called the coefficient group, and
is an arbitrary Abelian group, called the coefficient group, and 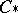 is a chain group, i.e. a graded Abelian group equipped with an endomorphism
is a chain group, i.e. a graded Abelian group equipped with an endomorphism 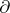 of degree
of degree 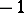 (the boundary mapping or boundary) with
(the boundary mapping or boundary) with 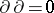 . In this situation the mapping
. In this situation the mapping  on the group
on the group 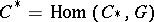 is defined as the adjoint of
is defined as the adjoint of 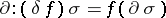 , where
, where 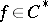 ,
, 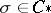 .
.
Given a topological space 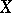 , one defines the group
, one defines the group 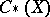 of singular chains as the Abelian group of formal finite sums
of singular chains as the Abelian group of formal finite sums 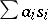 , where
, where 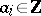 and the
and the 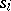 are arbitrary singular simplices in
are arbitrary singular simplices in 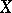 , i.e. continuous mappings of the standard simplex into
, i.e. continuous mappings of the standard simplex into 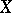 . A singular cochain in
. A singular cochain in 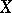 with coefficients in
with coefficients in 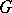 is defined as a homogeneous element of the group
is defined as a homogeneous element of the group  .
.
Similarly, a simplicial  -cochain of a simplicial complex in
-cochain of a simplicial complex in 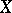 with coefficients in an Abelian group
with coefficients in an Abelian group 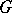 is defined as a homomorphism
is defined as a homomorphism 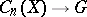 , where
, where 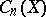 is the group of
is the group of  -chains of
-chains of 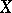 , i.e. the group of formal finite sums
, i.e. the group of formal finite sums  , where
, where 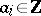 and the
and the 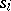 are
are  -simplices in
-simplices in 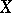 . In particular, a cochain in the sense of Aleksandrov–Čech in an arbitrary topological space
. In particular, a cochain in the sense of Aleksandrov–Čech in an arbitrary topological space  is a cochain of the nerve of an open covering of
is a cochain of the nerve of an open covering of 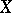 .
.
If 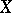 is a
is a 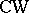 -complex (and
-complex (and 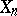 denotes the
denotes the  -skeleton of
-skeleton of 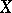 ), then the Abelian group
), then the Abelian group 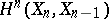 is called the group of
is called the group of  -dimensional cellular cochains of the complex
-dimensional cellular cochains of the complex  . The coboundary homomorphism
. The coboundary homomorphism 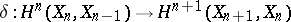 is put equal to the connecting mappings of the triple
is put equal to the connecting mappings of the triple 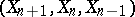 .
.
In practice, the group 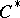 is frequently provided with an additional multiplicative structure, i.e. it is a graded algebra. In these cases the coboundary mapping
is frequently provided with an additional multiplicative structure, i.e. it is a graded algebra. In these cases the coboundary mapping 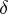 possesses the Leibniz property:
possesses the Leibniz property: 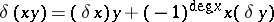 , where the element
, where the element 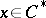 is assumed to be homogeneous of degree
is assumed to be homogeneous of degree 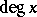 . An example of such a graded cochain algebra is the algebra of differential forms on a smooth manifold, in which the exterior differential acts as coboundary.
. An example of such a graded cochain algebra is the algebra of differential forms on a smooth manifold, in which the exterior differential acts as coboundary.
References
| [1] | P.J. Hilton, S. Wylie, "Homology theory. An introduction to algebraic topology" , Cambridge Univ. Press (1960) |
| [2] | S. MacLane, "Homology" , Springer (1963) |
Comments
References
| [a1] | N.E. Steenrod, S. Eilenberg, "Foundations of algebraic topology" , Princeton Univ. Press (1966) |
| [a2] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) |
| [a3] | C.R.F. Maunder, "Algebraic topology" , v. Nostrand-Reinhold (1970) |
Cochain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cochain&oldid=17694