Cobordism of knots

knot cobordism (proper bordism of knots, see Bordism)

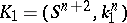An equivalence relation on the set of knots, weaker than the isotopy type relation. Two smooth -dimensional knots and 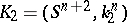are said to be cobordant if there exists a smooth oriented 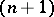-dimensional submanifold 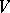of 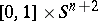, where 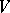is homeomorphic to and 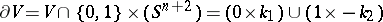. Here the minus sign indicates the opposite orientation. Knots cobordant to the trivial knot are called cobordant to zero, or slice knots. The set of (cobordance) equivalence classes of -dimensional smooth knots is denoted by 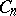. The operation of connected sum defines on 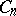an Abelian group structure. The inverse of the knot cobordism class 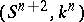is the knot cobordism class .

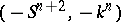For every even the group 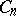is zero. The knot cobordism class of an odd-dimensional knot is defined by its Seifert matrix. A square integral matrix 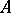is called cobordant to zero if it is unimodularly congruent to a matrix of the form

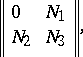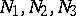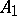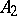where are square matrices of the same dimensions and 0 is the zero matrix. Two square matrices and are called cobordant if the matrix

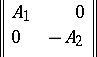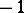is cobordant to zero. A square integral matrix is called an -matrix, where or , if 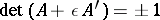. The Seifert matrix of every 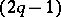-dimensional knot is a 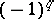-matrix. For every the cobordance relation is an equivalence relation on the set of all -matrices. The set of equivalence classes is denoted by 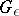. The operation of direct sum defines on 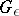an Abelian group structure. One has the Levine homomorphism 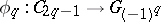which associates with the cobordism class of the knot 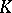the cobordism class of the Seifert matrix of 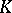. The Levine homomorphism is an isomorphism for all 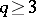. The homomorphism 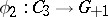is a monomorphism, its image is a subgroup of index 2 in 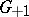, consisting of the class of 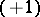-matrices 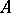for which the signature of 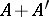is divisible by 16. The homomorphism 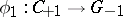is an epimorphism; its kernel is non-trivial.

For a study of the structure of the groups 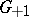and 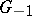and for the construction of a complete system of invariants of knot cobordism classes one makes use of the following construction. An isometric structure over a field 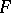is a pair 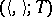consisting of a non-degenerate quadratic form 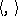given on a finite-dimensional vector space 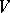over 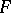and an isometry 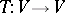. An isometric structure 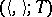is called cobordant to zero if 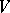contains a totally-isotropic subspace of half its dimension that is invariant under 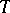. The operation of orthogonal sum of forms and direct sum of isometries defines an operation 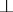on the set of isometric structures. Two isometric structures 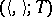and 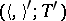are called cobordant if the isometric structure is cobordant to zero. Let 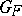be the set of cobordism classes of isometric structures 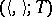satisfying the condition 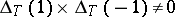, where 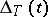is the characteristic polynomial of the isometry 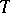. In the study of the groups 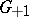and 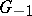an important role is played by the imbeddings 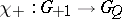and 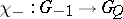, which are constructed as follows. Every cobordism class of -matrices contains a non-degenerate matrix. If 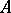is a non-degenerate -matrix, put 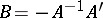, 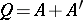and let 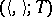be the isometric structure whose form 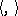has the given matrix 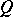, while its isometry 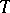has the matrix 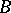. This gives a well-defined homomorphism 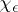with .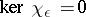

Let 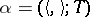be an isometric structure on a vector space 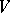and let 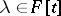. Denote by 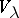the 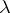-primary component of 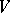, i.e. 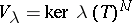for large 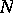. A polynomial 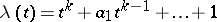is called reciprocal if for all 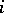. For each irreducible reciprocal polynomial 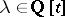denote by 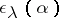the exponent, reduced modulo 2, with which 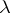divides the characteristic polynomial 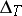of the isometry 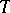. For every reciprocal polynomial 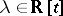irreducible over 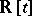, denote by 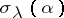the signature of the restriction of to 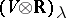. For each prime number 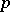and each reciprocal polynomial 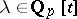irreducible over 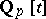, denote by 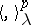the restriction of 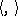to 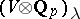, where 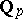is the field of 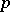-adic numbers. Put

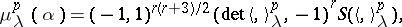where 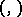is the Hilbert symbol in 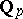, is the Hasse symbol and 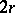is the rank of 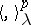. Two isometric structures 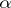and 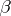are cobordant if and only if 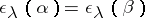, and 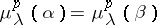for all 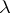and 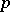for which these invariants are defined (cf. [3], [4]).

The compositions of the Levine homomorphism, the homomorphism 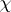and the functions 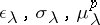associate with every odd-dimensional knot 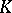the numbers 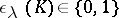, , 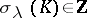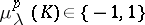. Two 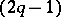-dimensional knots 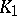and 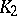, where 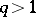, are cobordant if and only if

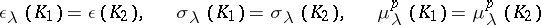for all 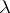and 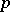for which these invariants are defined. 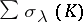is equal to the signature of the knot 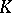(cf. Knots and links, quadratic forms of), where the sum is extended over all 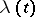of the form 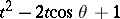, where 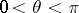, and in the sum only a finite number of terms are distinct from zero.

Similarly one defines the group of locally flat or piecewise-linear knot cobordisms, denoted by 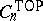and 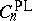, respectively. For all one has an isomorphism 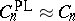. The natural mapping 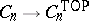is an isomorphism for 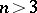, while for 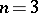it is a monomorphism with an image of index 2. This means, in particular, that there exists a non-smooth locally flat topologically three-dimensional knot in 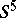(cf. [5]).

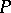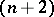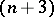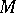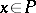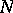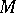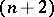The theory of cobordism of knots is connected with the study of singularities of not locally flat or piecewise-linear imbeddings of codimension 2. If is an -dimensional oriented manifold, imbedded as a subcomplex in an -dimensional manifold , , and is a small star-shaped neighbourhood of in , then the singularity of the imbedding of in at may be measured as follows. The boundary is an -dimensional sphere, the orientation of which is defined by that of 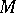; 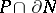is an -dimensional sphere the orientation of which is defined by that of 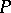. This defines an -dimensional knot 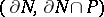, called the singularity of the imbedding at the point .

References

[1]	R.H. Fox, J.W. Milnor, "Singularities of 2-spheres in 4-space and cobordism of knots" Osaka Math. J. , 3 (1966) pp. 257–267
[2]	M.A. Kervaire, "Les noeuds de dimensions supérieures" Bull. Soc. Math. France , 93 (1965) pp. 225–271
[3]	J. Levine, "Knot cobordism groups in codimension 2" Comment. Math. Helv. , 44 (1969) pp. 229–244
[4]	J. Levine, "Invariants of knot cobordism" Invent. Math. , 8 (1969) pp. 98–110
[5]	S.E. Capell, J.L. Shaneson, "Topological knots and knot cobordism" Topology , 12 (1973) pp. 33–40
[6]	N.W. Stoltzfus, "Unraveling the integral knot concordance group" Mem. Amer. Math. Soc. , 12 (1977) pp. 192

Comments

Another term for cobordance of knots is concordance of knots, and correspondingly one has the knot concordance group.

References

[a1]	L.H. Kaufmann, "On knots" , Princeton Univ. Press (1987)