Closed operator
An operator  such that if
such that if  ,
,  and
and  , then
, then  and
and  . (Here
. (Here  are Banach spaces over the same field of scalars and
are Banach spaces over the same field of scalars and  is the domain of definition of
is the domain of definition of  .) The notion of a closed operator may be extended to operators defined on separable linear topological spaces, except that instead of a sequence
.) The notion of a closed operator may be extended to operators defined on separable linear topological spaces, except that instead of a sequence 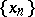 one must consider arbitrary directions (nets)
one must consider arbitrary directions (nets) 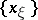 . If
. If 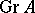 is the graph of
is the graph of 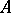 , then
, then 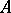 is closed if and only if
is closed if and only if 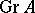 is a closed subset of the Cartesian product
is a closed subset of the Cartesian product 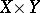 . This property is often adopted as the definition of a closed operator.
. This property is often adopted as the definition of a closed operator.
The notion of a closed operator is a generalization of the notion of an operator defined and continuous on a closed subset of a Banach space. An example of a closed but not continuous operator is  , defined on the set
, defined on the set  of continuously-differentiable functions in the space
of continuously-differentiable functions in the space 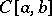 . Many operators of mathematical physics are closed but not continuous.
. Many operators of mathematical physics are closed but not continuous.
An operator  has a closure (i.e. is closeable) if it admits a closed extension. An operator has a closure if and only if it follows from
has a closure (i.e. is closeable) if it admits a closed extension. An operator has a closure if and only if it follows from 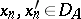 ,
,
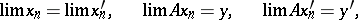 |
that 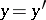 . The smallest closed extension of an operator is called its closure. A symmetric operator on a Hilbert space with dense domain of definition always admits a closure.
. The smallest closed extension of an operator is called its closure. A symmetric operator on a Hilbert space with dense domain of definition always admits a closure.
A bounded linear operator 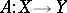 is closed. Conversely, if
is closed. Conversely, if 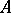 is defined on all of
is defined on all of 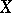 and closed, then it is bounded. If
and closed, then it is bounded. If 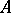 is closed and
is closed and 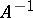 exists, then
exists, then  is also closed. Since
is also closed. Since 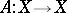 is closed if and only if
is closed if and only if 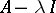 is closed, it follows that
is closed, it follows that 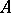 is closed if the resolvent
is closed if the resolvent 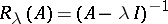 exists and is bounded for at least one value of the parameter
exists and is bounded for at least one value of the parameter 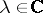 .
.
If 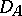 is dense in
is dense in 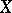 and, consequently, the adjoint operator
and, consequently, the adjoint operator 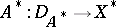 ,
, 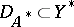 , is uniquely defined, then
, is uniquely defined, then 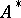 is a closed operator. If, moreover,
is a closed operator. If, moreover,  is dense in
is dense in  and
and 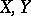 are reflexive, then
are reflexive, then 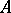 is a closeable operator and its closure is
is a closeable operator and its closure is 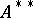 .
.
A closed operator can be made bounded by introducing a new norm on its domain of definition. Let
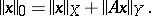 |
Then 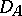 with this new norm is a Banach space and
with this new norm is a Banach space and 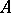 , as an operator from
, as an operator from  to
to 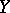 , is bounded.
, is bounded.
References
| [1] | K. Yosida, "Functional analysis" , Springer (1980) |
| [2] | T. Kato, "Perturbation theory for linear operators" , Springer (1980) |
Comments
The result that a closed linear operator mapping (all of) a Banach space into a Banach space is continuous is known as the closed-graph theorem.
References
| [a1] | S. Goldberg, "Unbounded linear operators" , McGraw-Hill (1966) |
Closed operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Closed_operator&oldid=11562