Closed geodesic
A closed smooth curve on a Riemannian manifold  that is a geodesic line. A more general notion is that of a geodesic loop, i.e. a geodesic
that is a geodesic line. A more general notion is that of a geodesic loop, i.e. a geodesic  (
( ) passing through the same point
) passing through the same point  at
at  and
and  ; considered as a closed curve, it may have an angle at
; considered as a closed curve, it may have an angle at  . A geodesic loop is a closed geodesic only if it has no angle, i.e. if
. A geodesic loop is a closed geodesic only if it has no angle, i.e. if  has the same tangent at
has the same tangent at  and
and  . Closed trajectories of the geodesic flow in the tangent bundle
. Closed trajectories of the geodesic flow in the tangent bundle  of
of  are projected onto closed geodesics under the natural projection
are projected onto closed geodesics under the natural projection  . The curve obtained when the same closed geodesic is traversed several times is called a multiple closed geodesic. A closed geodesic that is not multiple is called a simple closed geodesic.
. The curve obtained when the same closed geodesic is traversed several times is called a multiple closed geodesic. A closed geodesic that is not multiple is called a simple closed geodesic.
The definition of a closed geodesic and a geodesic loop carries over word for word to the case in which  is equipped with a Finsler metric or an affine connection. If
is equipped with a Finsler metric or an affine connection. If  is a metric space (in that case geodesic lines are defined as locally shortest lines), the definition of a geodesic loop remains the same, but that of a closed geodesic must be slightly modified since the notion of smoothness or angle are non-existent. A geodesic loop
is a metric space (in that case geodesic lines are defined as locally shortest lines), the definition of a geodesic loop remains the same, but that of a closed geodesic must be slightly modified since the notion of smoothness or angle are non-existent. A geodesic loop  (
( ), with
), with  and
and 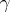 not constant on any subinterval, is a closed geodesic if, for sufficiently small
not constant on any subinterval, is a closed geodesic if, for sufficiently small 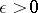 , the line
, the line
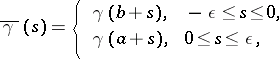 |
i.e. the union of two arcs of  : the first joining
: the first joining  to
to  , the second joining
, the second joining 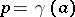 to
to 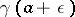 , is the shortest line between its end points
, is the shortest line between its end points  and
and  .
.
Closed geodesics have been investigated mainly in the case of closed Riemannian manifolds; there are also various results for Finsler manifolds; some results have been obtained in the more general case of metric spaces with certain special properties (known as Busemann  -spaces; see Geodesic geometry) [1]. These studies were initiated by J. Hadamard [2], H. Poincaré [3] and G. Birkhoff [4].
-spaces; see Geodesic geometry) [1]. These studies were initiated by J. Hadamard [2], H. Poincaré [3] and G. Birkhoff [4].
Hadamard was the pioneer in research on (not necessarily closed) geodesic lines on manifolds of negative curvature. The principal modern results relate to the case of closed manifolds  the curvature of which is negative in all two-dimensional directions at all points. For closed geodesics on such manifolds
the curvature of which is negative in all two-dimensional directions at all points. For closed geodesics on such manifolds 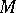 it has been proved that the closed trajectories of a geodesic flow are everywhere dense in
it has been proved that the closed trajectories of a geodesic flow are everywhere dense in  (see [5]) (an analogous phenomenon has been observed in several examples with positive curvature, though not always [6]); there exists an estimate for the growth of the number of closed geodesics of length not exceeding
(see [5]) (an analogous phenomenon has been observed in several examples with positive curvature, though not always [6]); there exists an estimate for the growth of the number of closed geodesics of length not exceeding 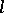 , as a function of increasing
, as a function of increasing 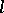 (see [7]). Hadamard approximated long segments of non-closed geodesics by closed geodesics — this can be regarded as the beginning of symbolic dynamics.
(see [7]). Hadamard approximated long segments of non-closed geodesics by closed geodesics — this can be regarded as the beginning of symbolic dynamics.
Another theorem due to Hadamard provides some information on closed geodesics on a closed manifold  (with no assumptions concerning its curvature) in terms of the properties of the fundamental group
(with no assumptions concerning its curvature) in terms of the properties of the fundamental group 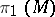 . An oriented closed curve
. An oriented closed curve  defines a certain conjugacy class
defines a certain conjugacy class 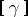 in
in 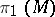 ; all curves in the same conjugacy class may be derived from one another by a free homotopy of curves. It turns out that, for every conjugacy class
; all curves in the same conjugacy class may be derived from one another by a free homotopy of curves. It turns out that, for every conjugacy class  of
of  , except the conjugacy class corresponding to the identity element, the set of closed curves
, except the conjugacy class corresponding to the identity element, the set of closed curves 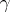 with
with 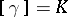 contains shortest members, and these shortest curves are closed geodesics. This theorem (which is valid not only for Riemannian or Finsler metrics, but also in the general case of Busemann
contains shortest members, and these shortest curves are closed geodesics. This theorem (which is valid not only for Riemannian or Finsler metrics, but also in the general case of Busemann  -spaces) is the simplest and historically the first result of the variational calculus in the large. However, the latter arose as an independent field of research from a more sophisticated application of variational methods to the study of closed geodesics on manifolds homeomorphic to a sphere, for which (as, in general, for simply-connected manifolds) the above theorem is meaningless.
-spaces) is the simplest and historically the first result of the variational calculus in the large. However, the latter arose as an independent field of research from a more sophisticated application of variational methods to the study of closed geodesics on manifolds homeomorphic to a sphere, for which (as, in general, for simply-connected manifolds) the above theorem is meaningless.
The study of closed geodesics on such manifolds was proposed by Poincaré (to be precise: He was concerned with an ovaloid, i.e. a two-dimensional closed convex surface). In the light of the discussion in [3], the following conjecture arose: In the "general" case, there exist three closed geodesics without self-intersections on an ovaloid; two of them are stable in the linear approximation, while the other is unstable. This connection between the existence of closed geodesics and the estimation of their number with the question of their stability properties constitutes an essential feature of Poincaré's heuristic arguments, which mainly were related to the theory of dynamical systems. These arguments may be carried out on a perfectly rigorous level, but only for metrics which are sufficiently close to the "standard" metric (the ordinary metric on the sphere  in Euclidean space; see [8]). For metrics far away from the standard metric, the stability properties postulated by Poincaré for closed geodesics need not be valid [9].
in Euclidean space; see [8]). For metrics far away from the standard metric, the stability properties postulated by Poincaré for closed geodesics need not be valid [9].
The credit for the initiation of the variational approach to closed geodesics on simply-connected manifolds is due to Birkhoff [4]. He proved that there is at least one closed geodesic on a manifold homeomorphic to a sphere. Later, Poincaré's conjecture concerning the existence of three non-self-intersecting closed geodesics on the two-dimensional sphere was proved by L.A. Lyusternik and L.G. Shnirel'man (see [10]).
Research has been done on the properties of closed geodesics for "typical" Riemannian (or Finsler) metrics (i.e. metrics forming sets of the second category in the space of all metrics of a given smoothness class) (see [11]–[13], [16]).
The standard metric on the sphere possesses the property that all its geodesics are closed and of the same length; there are also other metrics on the sphere with this property [14]. Consideration has also been given to the question of the topological properties of manifolds and their metrics when the latter have the above-mentioned property or some variant thereof.
A detailed exposition of the theory of closed geodesics may be found in [15].
References
| [1] | H. Busemann, "The geometry of geodesics" , Acad. Press (1955) |
| [2] | J. Hadamard, "Les surfaces à courbures opposées et leurs lignes géodésique" J. Math. Pure Appl. , 4 (1898) pp. 27–75 |
| [3] | H. Poincaré, "Sur les lignes géodésiques des surfaces convexes" Trans. Amer. Math. Soc. , 6 (1904) pp. 237–274 |
| [4] | G.D. Birkhoff, "Dynamical systems with two degrees of freedom" Trans. Amer. Math. Soc. , 18 (1917) pp. 199–300 |
| [5] | D.V. Anosov, "Geodesic flows on closed Riemannian manifolds with negative curvature" Proc. Steklov. Inst. Math. , 90 (1969) pp. 235 (Translated from Russian) |
| [6] | A.D. Weinstein, "Sur la non-densité des géodésiques fermées" C.R. Acad. Sci. Paris Ser. A , 271 (1970) pp. 504 |
| [7] | Ya.G. Sinai, "Asymptotic behaviour of closed geodesics on compact manifolds with negative curvature" Izv. Akad. Nauk SSSR Ser. Mat. , 30 : 6 (1966) pp. 1275–1296 (In Russian) |
| [8] | A.I. Gryuntal', "On closed self-intersecting geodesics on surfaces close to a sphere" Uspekhi Mat. Nauk , 32 : 4 (1977) pp. 244–245 (In Russian) |
| [9] | A.I. Gryuntal', "The existence of a metric on the two-dimensional sphere all closed self-intersecting geodesics of which are hyperbolic" Uspekhi Mat. Nauk , 32 : 5 (1977) pp. 166 (In Russian) |
| [10] | L.A. Lyusternik, L.G. Shnirel'man, "Topological methods in variational problems and their applications to the differential geometry of surfaces" Uspekhi Mat. Nauk , 2 : 1 (1947) pp. 166–217 (In Russian) |
| [11] | R. Abraham, "Bumpy metrics" S.-S. Chern (ed.) S. Smale (ed.) , Global analysis , Proc. Symp. Pure Math. , 14 , Amer. Math. Soc. (1970) pp. 1–3 |
| [12] | W. Klingenberg, F. Takens, "Generic properties of geodesic flows" Math. Ann. , 197 : 4 (1972) pp. 323–334 |
| [13] | W. Klingenberg, "Existence of infinitely many closed geodesics" J. Diff. Geom. , 11 (1976) pp. 299–308 |
| [14] | O. Zoll, "Ueber Flächen mit Scharen geschlossener geodetischer Linien" Math. Ann. , 57 (1903) pp. 108–133 |
| [15] | W. Klingenberg, "Lectures on closed geodesics" , Springer (1978) |
| [16] | D.V. Anosov, "On generic properties of closed geodesics" Math. USSR-Izv. , 21 : 1 (1983) pp. 1–29 Izv. Akad. Nauk SSSR Ser. Mat. , 46 : 4 (1982) pp. 675–709 |
Comments
A closed manifold 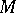 whose curvature is negative in all two-dimensional directions at all points is said said to have negative sectional curvature. (Analogously one defines positive sectional curvature.)
whose curvature is negative in all two-dimensional directions at all points is said said to have negative sectional curvature. (Analogously one defines positive sectional curvature.)
A free homotopy of a path or loop is simply a homotopy without the requirement that a certain base point be fixed.
The celebrated Lyusternik–Fet theorem ([a1]) says that on every compact Riemannian manifold  there exists a closed geodesic, extending the Birkhoff result. A systematic study of the study of closed curves on a compact Riemannian manifold was initiated by M. Morse. His main result was to characterize the closed geodesics among the closed curves as the non-constant critical points of the energy integral. A modern and refined version of this approach is due to W. Klingenberg: The space of closed curves of class
there exists a closed geodesic, extending the Birkhoff result. A systematic study of the study of closed curves on a compact Riemannian manifold was initiated by M. Morse. His main result was to characterize the closed geodesics among the closed curves as the non-constant critical points of the energy integral. A modern and refined version of this approach is due to W. Klingenberg: The space of closed curves of class 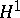 on a compact Riemannian manifold
on a compact Riemannian manifold 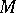 is in a canonical manner a Hilbert manifold
is in a canonical manner a Hilbert manifold  with Riemannian metric having the energy integral as differentiable function and endowed with a canonical
with Riemannian metric having the energy integral as differentiable function and endowed with a canonical  -action which corresponds to the various parameterizations of the unit circle. With this approach it can be shown that — at least generically — there always exist infinitely many closed geodesics on
-action which corresponds to the various parameterizations of the unit circle. With this approach it can be shown that — at least generically — there always exist infinitely many closed geodesics on  if
if  is simply connected. This is true even for all metrics on
is simply connected. This is true even for all metrics on 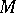 if the sequence
if the sequence  of Betti numbers of
of Betti numbers of  is unbounded, as was shown by D. Gromoll and W. Meyer (the Gromoll–Meyer theorem on closed geodesics, [a2]). For a detailed exposition see [15].
is unbounded, as was shown by D. Gromoll and W. Meyer (the Gromoll–Meyer theorem on closed geodesics, [a2]). For a detailed exposition see [15].
References
| [a1] | L.A. Lyusternik, A.I. Fet, "Variational problems on closed manifolds" Dokl. Akad. Nauk. SSSR , 81 (1951) pp. 17–18 (In Russian) |
| [a2] | D. Gromoll, W. Meyer, "Periodic geodesics on compact Riemannian manifolds" J. Diff. Geom. , 8 (1973) pp. 207–223 |
Closed geodesic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Closed_geodesic&oldid=19129