Clausius-Duhem inequality
Named after one of the founding fathers of irreversible thermodynamics, R. Clausius, and the famed proponent of energeticism, P. Duhem, the Clausius–Duhem inequality is essentially a global statement of the second law of continuum thermodynamics in the following form:
 | (a1) |
Here, 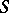 is the total entropy pertaining to the actual volume
is the total entropy pertaining to the actual volume 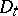 occupied by a material body at time
occupied by a material body at time 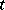 in physical Euclidean space
in physical Euclidean space 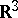 ,
,  being its, supposedly regular, boundary and
being its, supposedly regular, boundary and 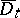 its closure. The scalar
its closure. The scalar 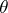 such that
such that 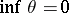 ,
, 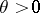 , is the so-called thermodynamical temperature,
, is the so-called thermodynamical temperature, 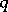 is the heat flux per unit area,
is the heat flux per unit area, 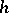 is the mass density of heat by radiation, a superimposed dot indicates the material time derivative, and
is the mass density of heat by radiation, a superimposed dot indicates the material time derivative, and  is the mass element if
is the mass element if 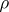 is the matter density at the actual placement
is the matter density at the actual placement  at absolute time
at absolute time  of a material point
of a material point 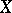 of the material differentiable manifold
of the material differentiable manifold 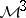 . Clausius' original form of (a1) had zero for the right-hand side. The surface contribution was added by Duhem [a1], and the bulk term by C.A. Truesdell and R.A. Toupin [a2]. (a1) holds when the thermodynamical evolution is such that the relation between two nearby thermodynamical states not necessarily in equilibrium satisfies the axiom of local state. This axiom states that the response times inherent in perturbations of a thermal equilibrium, and permitting a subsystem such as
. Clausius' original form of (a1) had zero for the right-hand side. The surface contribution was added by Duhem [a1], and the bulk term by C.A. Truesdell and R.A. Toupin [a2]. (a1) holds when the thermodynamical evolution is such that the relation between two nearby thermodynamical states not necessarily in equilibrium satisfies the axiom of local state. This axiom states that the response times inherent in perturbations of a thermal equilibrium, and permitting a subsystem such as 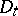 to revert to a new thermodynamical state, are supposed to be much less than the characteristic times of the kinematical and dynamical evolutions of this subsystem. Consequently, one attributes to entropy its equilibrium value, assuming that
to revert to a new thermodynamical state, are supposed to be much less than the characteristic times of the kinematical and dynamical evolutions of this subsystem. Consequently, one attributes to entropy its equilibrium value, assuming that 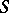 is differentiable in the appropriate time interval. Entropy being an extensive (proportional to mass) state variable, the specific entropy
is differentiable in the appropriate time interval. Entropy being an extensive (proportional to mass) state variable, the specific entropy 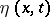 is introduced for sufficiently regular processes such that
is introduced for sufficiently regular processes such that
 | (a2) |
Application of the Cauchy tetrahedron argument in continuum physics to (a1) allows one to introduce the entropy flux and heat flux, 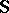 and
and 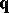 , respectively, such that
, respectively, such that 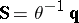 , and
, and  , where
, where 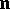 is the unit outward normal to
is the unit outward normal to  . The localization of (a1) for sufficiently regular fields then yields the following pointwise local expression of the Clausius–Duhem inequality:
. The localization of (a1) for sufficiently regular fields then yields the following pointwise local expression of the Clausius–Duhem inequality:
 | (a3) |
(a1) holds while the total energy is balanced (first law of thermodynamics). It has become customary to give the name Clausius–Duhem inequality, per se, to the expression of equation (a3) (also called the residual dissipation inequality) obtained on account of the local statement of the first law of thermodynamics and after introduction of the Helmholtz free energy 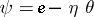 per unit mass at every point
per unit mass at every point 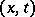 if
if  is the specific internal energy. E.g., for the so-called simple thermo-mechanical materials:
is the specific internal energy. E.g., for the so-called simple thermo-mechanical materials:
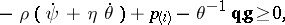 | (a4) |
where  , and
, and 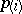 is the power expanded by internal forces, such that
is the power expanded by internal forces, such that  , where
, where  is the deformation gradient based on the motion
is the deformation gradient based on the motion 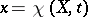 ,
, 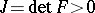 , and
, and 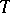 is the first Piola–Kirchhoff stress or engineering stress.
is the first Piola–Kirchhoff stress or engineering stress.
C. Eckart [a3] is considered to be the main original contributor to the notion of thermodynamical admissibility (a basic axiom of continuum physics), for which the Clausius–Duhem inequality (a3) or (a4) is viewed as a mathematical constraint on thermodynamical evolution. But B.D. Coleman and W. Noll [a4], viewing (a1) as an a priori postulate in true thermodynamics, are responsible for the idea that the Clausius–Duhem inequality should be interpreted as an identical restriction on constitutive relations (e.g., for 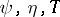 and
and 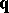 ) and as such should lead to a proof of the existence of thermodynamic potentials in certain cases (see [a5], [a6]; for generalizations to complex electromagnetic phenomena in continua, see [a7], to plasticity and fracture, see [a8], and to media with microstructure, see [a9]). The corresponding thermodynamics is often called Coleman–Noll thermodynamics.
) and as such should lead to a proof of the existence of thermodynamic potentials in certain cases (see [a5], [a6]; for generalizations to complex electromagnetic phenomena in continua, see [a7], to plasticity and fracture, see [a8], and to media with microstructure, see [a9]). The corresponding thermodynamics is often called Coleman–Noll thermodynamics.
I. Müller [a10] introduced a more general framework, where the entropy flux 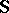 is no longer assumed in its classical form
is no longer assumed in its classical form 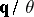 from the start, but is itself a constitutive field in need of a constitutive equation. Liu I-Shih [a11] has further elaborated on this by considering that the Clausius–Duhem inequality holds under the mathematical constraints of the field equations (e.g., balance of mass, momentum, energy) of the problem, so that these must be accounted for in the inequality statement through the introduction of Lagrange multipliers (see [a12], [a13]). The consideration of fluxes, such as stress and heat flux, as independent variables in the entropy function while they satisfy additional evolution-diffusion equations in agreement with some views of kinetic theory, then yields so-called extended irreversible thermodynamics, which allows for a better satisfaction of causality of the related wave problem (see [a14], [a15]).
from the start, but is itself a constitutive field in need of a constitutive equation. Liu I-Shih [a11] has further elaborated on this by considering that the Clausius–Duhem inequality holds under the mathematical constraints of the field equations (e.g., balance of mass, momentum, energy) of the problem, so that these must be accounted for in the inequality statement through the introduction of Lagrange multipliers (see [a12], [a13]). The consideration of fluxes, such as stress and heat flux, as independent variables in the entropy function while they satisfy additional evolution-diffusion equations in agreement with some views of kinetic theory, then yields so-called extended irreversible thermodynamics, which allows for a better satisfaction of causality of the related wave problem (see [a14], [a15]).
The "arrow of timearrow of time" dictated by the Clausius–Duhem inequality and causality, represented mathematically by the hyperbolicity of the studied system of field equations, once closed by the prescription of thermodynamically admissible constitutive equations, are thus inter-related.
References
| [a1] | P.M.-M. Duhem, "Traité d'énergétique ou de thermodynamique" , Gauthier-Villars (1911) |
| [a2] | C.A. Truesdell, R.A. Toupin, "The classical field theories" S. Flügge (ed.) , Handbuch der Physik , III/1 , Springer (1960) |
| [a3] | C. Eckart, "The thermodynamics of irreversible processes I. The simple fluid" Phys. Rev. , 58 (1940) pp. 267–269 |
| [a4] | B.D. Coleman, W. Noll, "The thermodynamics of elastic materials with conduction and viscosity" Arch. Rat. Mech. Anal. , 13 (1963) pp. 167–178 |
| [a5] | C.A. Truesdell, "Rational thermodynamics" , Springer, reprint (1986) |
| [a6] | A.C. Eringen, "Continuum physics" , 2 , Acad. Press (1975) |
| [a7] | G.A. Maugin, "Continuum mechanics of electromagnetic solids" , North-Holland (1988) |
| [a8] | G.A. Maugin, "The thermomechanics of plasticity and fracture" , Cambridge Univ. Press (1992) |
| [a9] | G.A. Maugin, W. Muschik, "Thermodynamics with internal variables" J. Non-Equilib. Thermodyn. , 19 (1994) pp. 217–289 |
| [a10] | I. Müller, "On the entropy inequality" Arch. Rat. Mech. Anal. , 26 (1967) pp. 118–141 |
| [a11] | I-Shih Liu, "Method of Lagrange multipliers for exploitation of the entropy principle" Arch. Rat. Mech. Anal. , 46 (1972) pp. 131–146 |
| [a12] | I. Müller, "Thermodynamics" , Pitman (1985) |
| [a13] | W. Muschik, "Aspects of non-equilibrium thermodynamics" , World Sci. (1990) |
| [a14] | I. Müller, T. Ruggeri, "Extended thermodynamics" , Springer (1993) |
| [a15] | D. Jou, J. Casas-Vasquez, G. Lebon, "Extended irreversible thermodynamics" , Springer (1996) (Edition: Second) |
Clausius-Duhem inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Clausius-Duhem_inequality&oldid=18182