Circle method

One of the most general methods in additive number theory. Let 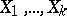be arbitrary sets of natural numbers, let 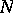be a natural number and let 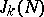be the number of solutions of the equation

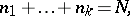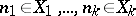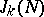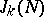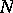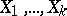where . It is with the investigation of the numbers that additive number theory is concerned; for example, if it can be proved that is greater than zero for all , this means that any natural number is the sum of terms taken respectively from the sets . Now let be a complex number, , and let

Then the function defined by

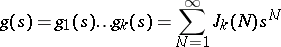is the generating function of the 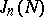. By Cauchy's formula,

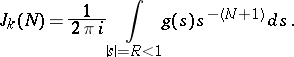The integral in this equality is investigated as . The circle of integration 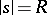is divided into "major" and "minor" arcs, the centres of which are rational numbers. There is a broad range of additive problems in which the integrals over "major" arcs, which yield a "principal" part of , can be investigated fairly completely, while the integrals over the "minor" arcs, which yield a "remainder" term in the asymptotic formula for 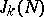, can be estimated.

I.M. Vinogradov's use of trigonometric sums in the circle method not only considerably simplified application of the method, it also provided a unified approach to the solution of a wide range of very different additive problems. The basis for the circle method in the form of trigonometric sums is the formula

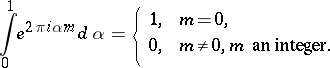It follows from this formula that

where

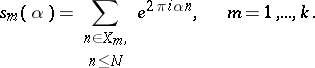The finite sums are called trigonometric sums. To investigate the 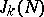, one divides the integration interval 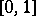into "major" and "minor" arcs, i.e. intervals centred at rational points with "small" and "large" denominators. For many additive problems one can successfully evaluate — with adequate accuracy — the integrals over the "major" arcs (the trigonometric sums for 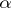in "major" arcs are close to rational trigonometric sums with small denominators, which are readily evaluated and are "large" ); as for the "minor" arcs, which contain the bulk of the points in 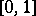, the trigonometric sums over these are "small" ; they can be estimated in a non-trivial manner (see Trigonometric sums, method of; Vinogradov method), so that asymptotic formulas can be established for .

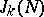The circle method in the trigonometric sum version, together with Vinogradov's method for estimating trigonometric sums, yields the strongest results of additive number theory (see Waring problem; Goldbach problem; Goldbach–Waring problem; Hilbert–Kamke problem).

References

[1]	I.M. Vinogradov, "The method of trigonometric sums in the theory of numbers" , Interscience (1954) (Translated from Russian)
[2]	L.-K. Hua, "The method of trigonometric sums and its applications to number theory" , Selected papers , Springer (1983) pp. 124–135 (Translated from German)
[3]	A.A. Karatsuba, "Fundamentals of analytic number theory" , Moscow (1975) (In Russian)

Comments

The circle method as described above is often referred to as the Hardy–Littlewood method or the Hardy–Littlewood circle method. The method can be adapted to a number of quite diverse situations. Some examples follow. The Davenport–Heilbron theorem says that if 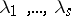, , are real numbers, not all of the same sign if 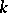is even, and such that at least one ratio 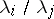is irrational, then for all there are integers , not all zero, such that . 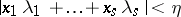Let 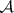be a subset of the natural numbers such that 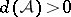, where 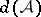is the upper asymptotic density. Then the Furstenberg–Sárközy theorem says that if 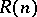is the number of solutions of 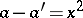with 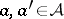, , 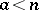, 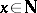then 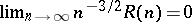. Finally there is e.g. Birch's theorem to the effect that the dimension of the space of simultaneous zeros of 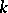homogeneous forms of odd degree grows arbitrarily large with the number of variables of those forms.

References

[a1]	R.C. Vaughan, "The Hardy–Littlewood method" , Cambridge Univ. Press (1981)