Christoffel symbol

of a differential quadratic form

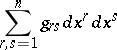An abbreviated notation for the expression

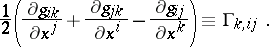The symbols are called the Christoffel symbols of the first kind, in contrast to the Christoffel symbols of the second kind, , defined by

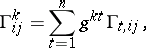where is defined as follows:

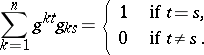These symbols were introduced by E.B. Christoffel in 1869.

Comments

Let , , be a linear connection on a manifold , where denotes the space of vector fields on . Let be a chart of . Then on , is completely determined by 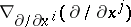, where are coordinates on . The Christoffel symbols of the connection are now given by

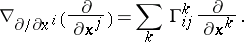It is important to note that the 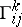are not the components of a tensor field. In fact if the denote the Christoffel symbols of with respect to a second set of coordinates on , then

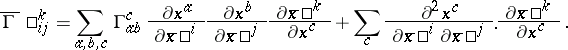Let now be the Riemannian connection (cf. Riemannian geometry) defined by a (local) Riemannian metric . Then the Christoffel symbols of this quadratic differential form are those of the connection . I.e.,

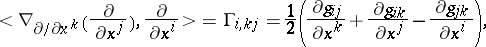so that indeed

where the 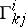are the Christoffel symbols of the second kind of the quadratic differential form as defined above.

References

[a1]	S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1 , Interscience (1963) pp. Chapt. 4
[a2]	R.S. Millman, G.D. Parker, "Elements of differential geometry" , Prentice-Hall (1977) pp. Chapt. 7