Christoffel-Schwarz formula
The formula
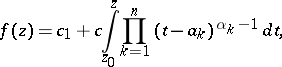 | (*) |
constituting an integral representation for a function 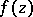 which defines a conformal mapping of the upper half-plane
which defines a conformal mapping of the upper half-plane  onto the interior of a bounded polygon with vertices
onto the interior of a bounded polygon with vertices 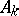 and vertex angles
and vertex angles 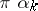 (
(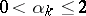 ,
,  ). Moreover,
). Moreover, 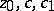 are certain constants, and
are certain constants, and  . The constant
. The constant 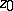 can be fixed arbitrarily in the upper half-plane. A triple of points in the sequence
can be fixed arbitrarily in the upper half-plane. A triple of points in the sequence  , say
, say 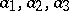 , can be prescribed arbitrarily; the remaining
, can be prescribed arbitrarily; the remaining 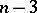 points
points 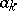 and the constants
and the constants 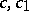 are uniquely determined if the vertices
are uniquely determined if the vertices 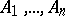 of the polygon are prescribed (see [3]). Formula (*) was established independently by E.B. Christoffel (1867, see ) and H.A. Schwarz (1869, see [2]). The integral on the right-hand side of (*) is known as a Christoffel–Schwarz integral.
of the polygon are prescribed (see [3]). Formula (*) was established independently by E.B. Christoffel (1867, see ) and H.A. Schwarz (1869, see [2]). The integral on the right-hand side of (*) is known as a Christoffel–Schwarz integral.
The basic difficulty in using formula (*) is to find the unknown parameters. No general methods are known for 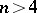 .
.
Methods have been worked out for approximating the parameters of the Christoffel–Schwarz formula (see [4], [5]).
The Christoffel–Schwarz formula remains valid for polygons with one or more vertices at infinity. In that case the angle between the sides at infinity is, by definition, the angle (with minus sign) between the relevant sides (or their continuations) at a finite point. If the pre-image 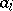 of one of the vertices is the point at infinity, the corresponding factor
of one of the vertices is the point at infinity, the corresponding factor 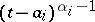 is dropped in formula (*).
is dropped in formula (*).
The Christoffel–Schwarz formula is also valid for a function that maps the unit disc 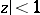 onto the above polygon. In that case
onto the above polygon. In that case  ,
, 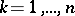 ,
, 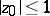 . Modifications of the formula are valid for functions mapping the upper half-plane — or the interior and exterior of the unit disc — onto the exterior of a polygon (see [3]).
. Modifications of the formula are valid for functions mapping the upper half-plane — or the interior and exterior of the unit disc — onto the exterior of a polygon (see [3]).
The Christoffel–Schwarz formula may be generalized to the case in which 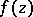 defines a conformal mapping of a circular annulus
defines a conformal mapping of a circular annulus 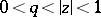 , or, in general, a multiply-connected domain defined by deleting
, or, in general, a multiply-connected domain defined by deleting  discs from the interior of a disc, onto a domain (multiply-connected of the same degree) bounded by polygons (see [6], [7]).
discs from the interior of a disc, onto a domain (multiply-connected of the same degree) bounded by polygons (see [6], [7]).
References
| [1a] | E.B. Christoffel, Ann. di Math. Pura Appl. (2) , 1 (1868) pp. 89–103 |
| [1b] | E.B. Christoffel, Ann. di Math. Pura Appl. (2) , 4 (1871) pp. 1–9 |
| [2] | H.A. Schwarz, "Gesamm. math. Abhandl." , 1–2 , Springer (1890) |
| [3] | M.A. Lavrent'ev, B.V. Shabat, "Methoden der komplexen Funktionentheorie" , Deutsch. Verlag Wissenschaft. (1967) (Translated from Russian) |
| [4] | L.V. Kantorovich, V.I. Krylov, "Approximate methods of higher analysis" , Noordhoff (1958) (Translated from Russian) |
| [5] | W. Koppenfels, F. Stalman, "Praxis der konformen Abbildung" , Springer (1959) |
| [6] | N.I. Akhiezer, "Elements of the theory of elliptic functions" , Amer. Math. Soc. (1990) (Translated from Russian) |
| [7] | Yu.D. Maksimov, "Extension of the structural formula for convex univalent functions to a multiply connected circular region" Soviet Math. Dokl. , 2 pp. 55–58 Dokl. Akad. Nauk SSSR , 136 : 2 (1961) pp. 284–287 |
Comments
The above formula is also called the Schwarz–Christoffel formula (cf. [a1]).
References
| [a1] | L.V. Ahlfors, "Complex analysis" , McGraw-Hill (1979) pp. Chapt. 6, Sect. 2 |
| [a2] | E. Hille, "Analytic function theory" , 2 , Chelsea, reprint (1977) |
| [a3] | Z. Nehari, "Conformal mapping" , Dover, reprint (1975) pp. 2 |
Christoffel-Schwarz formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Christoffel-Schwarz_formula&oldid=46343