Chi-squared test
A test for the verification of a hypothesis 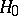 according to which a random vector of frequencies
according to which a random vector of frequencies 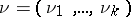 has a given polynomial distribution, characterized by a vector of positive probabilities
has a given polynomial distribution, characterized by a vector of positive probabilities 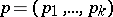 ,
, 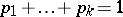 . The "chi-squared" test is based on the Pearson statistic
. The "chi-squared" test is based on the Pearson statistic
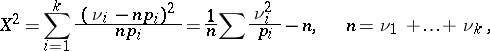 |
which has in the limit, as 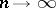 , a "chi-squared" distribution with
, a "chi-squared" distribution with 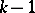 degrees of freedom, that is,
degrees of freedom, that is,
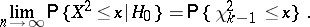 |
According to the "chi-squared" test with significance level 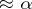 , the hypothesis
, the hypothesis 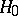 must be rejected if
must be rejected if 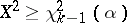 , where
, where 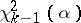 is the upper
is the upper 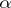 -quantile of the "chi-squared" distribution with
-quantile of the "chi-squared" distribution with 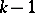 degrees of freedom, that is,
degrees of freedom, that is,
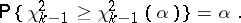 |
The statistic  is also used to verify the hypothesis
is also used to verify the hypothesis 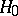 that the distribution functions of independent identically-distributed random variables
that the distribution functions of independent identically-distributed random variables 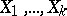 belong to a family of continuous functions
belong to a family of continuous functions 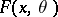 ,
, 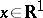 ,
, 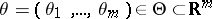 ,
, 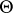 an open set. After dividing the real line by points
an open set. After dividing the real line by points 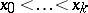 ,
, 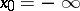 ,
, 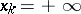 , into
, into  intervals
intervals 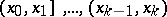 ,
, 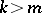 , such that for all
, such that for all  ,
,
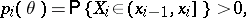 |
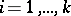 ;
; 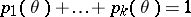 , one forms the frequency vector
, one forms the frequency vector 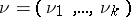 , which is obtained as a result of grouping the values of the random variables
, which is obtained as a result of grouping the values of the random variables 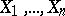 into these intervals. Let
into these intervals. Let
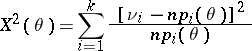 |
be a random variable depending on the unknown parameter 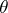 . To verify the hypothesis
. To verify the hypothesis 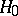 one uses the statistic
one uses the statistic 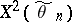 , where
, where 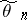 is an estimator of the parameter
is an estimator of the parameter 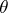 , computed by the method of the minimum of "chi-squared" , that is,
, computed by the method of the minimum of "chi-squared" , that is,
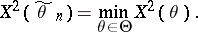 |
If the intervals of the grouping are chosen so that all 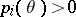 , if the functions
, if the functions 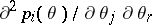 are continuous for all
are continuous for all 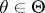 ,
, 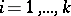 ;
; 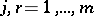 , and if the matrix
, and if the matrix  has rank
has rank  , then if the hypothesis
, then if the hypothesis 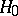 is valid and as
is valid and as  , the statistic
, the statistic 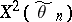 has in the limit a "chi-squared" distribution with
has in the limit a "chi-squared" distribution with  degrees of freedom, which can be used to verify
degrees of freedom, which can be used to verify 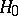 by the "chi-squared" test. If one substitutes a maximum-likelihood estimator
by the "chi-squared" test. If one substitutes a maximum-likelihood estimator 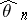 in
in  , computed from the non-grouped data
, computed from the non-grouped data 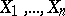 , then under the validity of
, then under the validity of  and as
and as 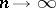 , the statistic
, the statistic 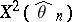 is distributed in the limit like
is distributed in the limit like
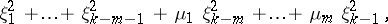 |
where 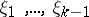 are independent standard normally-distributed random variables, and the numbers
are independent standard normally-distributed random variables, and the numbers 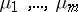 lie between 0 and 1 and, generally speaking, depend upon the unknown parameter
lie between 0 and 1 and, generally speaking, depend upon the unknown parameter 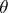 . From this it follows that the use of maximum-likelihood estimators in applications of the "chi-squared" test for the verification of the hypothesis
. From this it follows that the use of maximum-likelihood estimators in applications of the "chi-squared" test for the verification of the hypothesis 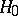 leads to difficulties connected with the computation of a non-standard limit distribution.
leads to difficulties connected with the computation of a non-standard limit distribution.
In [3]–[8] there are some recommendations concerning the 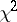 -test in this case; in particular, in the normal case [3], the general continuous case [4], [8], the discrete case [6], [8], and in the problem of several samples [7].
-test in this case; in particular, in the normal case [3], the general continuous case [4], [8], the discrete case [6], [8], and in the problem of several samples [7].
References
| [1] | M.G. Kendall, A. Stuart, "The advanced theory of statistics" , 2. Inference and relationship , Griffin (1983) |
| [2] | D.M. Chibisov, "Certain chi-square type tests for continuous distributions" Theory Probab. Appl. , 16 : 1 (1971) pp. 1–22 Teor. Veroyatnost. i Primenen. , 16 : 1 (1971) pp. 3–20 |
| [3] | M.S. Nikulin, "Chi-square test for continuous distributions with shift and scale parameters" Theory Probab. Appl. , 18 : 3 (1973) pp. 559–568 Teor. Veroyatnost. i Primenen. , 18 : 3 (1973) pp. 583–592 |
| [4] | K.O. Dzhaparidze, M.S. Nikulin, "On a modification of the standard statistics of Pearson" Theor. Probab. Appl. , 19 : 4 (1974) pp. 851–853 Teor. Veroyatnost. i Primenen. , 19 : 4 (1974) pp. 886–888 |
| [5] | M.S. Nikulin, "On a quantile test" Theory Probab. Appl. , 19 : 2 (1974) pp. 410–413 Teor. Veroyatnost. i Primenen. : 2 (1974) pp. 410–414 |
| [6] | L.N. Bol'shev, M. Mirvaliev, "Chi-square goodness-of-fit test for the Poisson, binomial and negative binomial distributions" Theory Probab. Appl. , 23 : 3 (1974) pp. 461–474 Teor. Veroyatnost. i Primenen. , 23 : 3 (1978) pp. 481–494 |
| [7] | L.N. Bol'shev, M.S. Nikulin, "A certain solution of the homogeneity problem" Serdica , 1 (1975) pp. 104–109 (In Russian) |
| [8] | P.E. Greenwood, M.S. Nikulin, "Investigations in the theory of probabilities distributions. X" Zap. Nauchn. Sem. Leningr. Otdel. Mat. Inst. Steklov. , 156 (1987) pp. 42–65 (In Russian) |
Comments
The "chi-squared" test is also called the "chi-square" test or 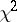 -test.
-test.
Chi-squared test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chi-squared_test&oldid=15852