Chevalley group
A linear algebraic group over some field, related to a semi-simple complex Lie algebra. Let 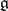 be a semi-simple algebra over
be a semi-simple algebra over 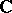 , let
, let 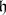 be its Cartan subalgebra, let
be its Cartan subalgebra, let  be a root system of
be a root system of 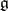 with respect to
with respect to  , let
, let 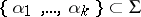 be a system of simple roots, let
be a system of simple roots, let 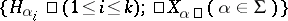 be a Chevalley basis of the algebra
be a Chevalley basis of the algebra 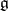 , and let
, and let 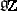 be its linear envelope over
be its linear envelope over 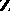 . Let
. Let 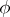 be a faithful representation of the Lie algebra
be a faithful representation of the Lie algebra 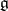 in a finite-dimensional vector space
in a finite-dimensional vector space 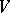 . It turns out that there is a lattice in
. It turns out that there is a lattice in 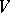 (i.e. a free Abelian subgroup a basis of which is the basis of the space
(i.e. a free Abelian subgroup a basis of which is the basis of the space 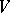 ) which is invariant with respect to all operators
) which is invariant with respect to all operators 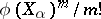 (
(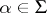 ,
, 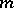 is a natural number). If
is a natural number). If 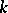 is an arbitrary field and if
is an arbitrary field and if 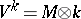 , then homomorphisms
, then homomorphisms 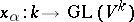 ,
, 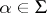 , are defined and are given by the formulas
, are defined and are given by the formulas
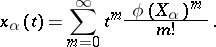 |
The subgroups 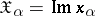 ,
, 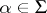 , generate in
, generate in 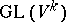 some subgroup
some subgroup 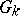 , which is called the Chevalley group related to the Lie algebra
, which is called the Chevalley group related to the Lie algebra 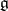 , the representation
, the representation 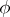 and the field
and the field 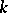 . If
. If 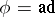 (the adjoint representation), the Chevalley groups were defined by C. Chevalley in 1955 (see [1]).
(the adjoint representation), the Chevalley groups were defined by C. Chevalley in 1955 (see [1]).
If 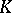 is an algebraically closed field containing
is an algebraically closed field containing 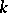 , then a Chevalley group
, then a Chevalley group 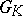 is a connected semi-simple linear algebraic group over
is a connected semi-simple linear algebraic group over 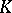 , defined and split over the prime subfield
, defined and split over the prime subfield 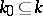 . Its Lie algebra is isomorphic to
. Its Lie algebra is isomorphic to 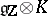 . The group
. The group 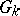 is the commutator subgroup of the group
is the commutator subgroup of the group 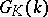 of points of
of points of 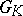 that are rational over
that are rational over 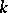 . Any connected semi-simple linear algebraic group over
. Any connected semi-simple linear algebraic group over  is isomorphic to one of the Chevalley groups. The algebraic groups
is isomorphic to one of the Chevalley groups. The algebraic groups 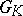 (and
(and 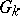 as abstract groups) depend only on the lattice
as abstract groups) depend only on the lattice  generated by the weights of the representation
generated by the weights of the representation 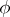 . If
. If  coincides with the lattice of roots
coincides with the lattice of roots 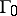 , then
, then 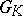 is called the adjoint group, and if
is called the adjoint group, and if 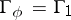 (the lattice of weights, see Lie group, semi-simple), then
(the lattice of weights, see Lie group, semi-simple), then 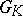 is called a universal or simply-connected group. If
is called a universal or simply-connected group. If 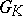 is universal, then
is universal, then 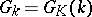 .
.
The Chevalley group 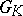 always coincides with its commutator subgroup. The centre of
always coincides with its commutator subgroup. The centre of  is finite. For example, the centre
is finite. For example, the centre 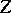 of the universal group
of the universal group 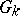 is isomorphic to
is isomorphic to  , and the corresponding adjoint group is isomorphic to
, and the corresponding adjoint group is isomorphic to 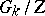 and has trivial centre.
and has trivial centre.
If the algebra 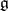 is simple, then the adjoint Chevalley group
is simple, then the adjoint Chevalley group 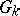 is simple, except in the following cases:
is simple, except in the following cases:  and
and 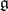 is a Lie algebra of type
is a Lie algebra of type 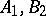 or
or 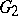 ; or
; or  and
and 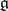 is a Lie algebra of type
is a Lie algebra of type 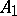 . Other series of simple groups can be obtained when considering the subgroups of fixed points of certain automorphisms of finite order of Chevalley groups (so-called torsion groups).
. Other series of simple groups can be obtained when considering the subgroups of fixed points of certain automorphisms of finite order of Chevalley groups (so-called torsion groups).
If the field 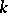 is finite, then the order of the universal group
is finite, then the order of the universal group 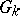 can be computed by the formula
can be computed by the formula
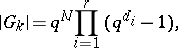 |
where 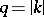 ,
, 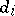 (
(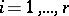 ) are exponents of the Lie algebra
) are exponents of the Lie algebra 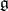 , i.e. the degrees of the free polynomials on
, i.e. the degrees of the free polynomials on  , generating the algebras, that are invariant with respect to the Weyl group, and
, generating the algebras, that are invariant with respect to the Weyl group, and 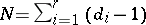 is the number of positive roots.
is the number of positive roots.
There is a well-developed theory of rational linear representations of the Chevalley groups 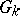 over an infinite field
over an infinite field 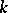 . It is reduced to the case of an algebraically closed field, and in the latter case coincides with the theory of rational representations (cf. Rational representation) of semi-simple algebraic groups. If
. It is reduced to the case of an algebraically closed field, and in the latter case coincides with the theory of rational representations (cf. Rational representation) of semi-simple algebraic groups. If 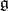 is simple,
is simple,  is the universal Chevalley group over the infinite field
is the universal Chevalley group over the infinite field  , and
, and  is a non-trivial irreducible finite-dimensional representation of
is a non-trivial irreducible finite-dimensional representation of  (as an abstract group) over an algebraically closed field
(as an abstract group) over an algebraically closed field 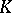 , then there exists a finite set of imbeddings
, then there exists a finite set of imbeddings 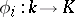 and a set of rational representations
and a set of rational representations  of the groups
of the groups 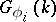 such that
such that 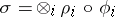 . Concerning representations of Chevalley groups, see also [2], [3], [5].
. Concerning representations of Chevalley groups, see also [2], [3], [5].
References
| [1] | C. Chevalley, "Sur certains groupes simples" Tôhoku Math. J. , 7 : 1–2 (1955) pp. 14–66 |
| [2] | R.G. Steinberg, "Lectures on Chevalley groups" , Yale Univ. Press (1968) |
| [3] | A. Borel (ed.) R. Carter (ed.) C.W. Curtis (ed.) N. Iwahori (ed.) T.A. Springer (ed.) R. Steinberg (ed.) , Seminar on algebraic groups and related finite groups , Lect. notes in math. , 131 , Springer (1970) |
| [4] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) |
| [5] | J.E. Humphreys, "Ordinary and modular representations of Chevalley groups" , Springer (1976) |
Comments
In the above 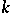 denotes the characteristic of the field
denotes the characteristic of the field 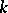 .
.
The torsion groups are also called the twisted Chevalley groups or the Steinberg groups. They were introduced by R. Steinberg in [a1].
An important reference for the representation theory of Chevalley groups is the recent textbook by R.W. Carter [a2].
References
| [a1] | R. Steinberg, "Variations on a theme of Chevalley" Pacific J. Math. , 9 (1959) pp. 875–891 |
| [a2] | R.W. Carter, "Finite groups of Lie type: Conjugacy classes and complex characters" , Wiley (Interscience) (1985) |
Chevalley group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chevalley_group&oldid=16653