Chern number
A characteristic number of a quasi-complex manifold. Let 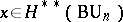 be an arbitrary characteristic class. For a closed quasi-complex manifold
be an arbitrary characteristic class. For a closed quasi-complex manifold 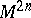 the integer
the integer 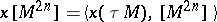 is called the Chern number of the manifold
is called the Chern number of the manifold 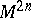 corresponding to the class
corresponding to the class  . Here
. Here 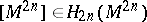 is the fundamental class of the manifold, or the orientation, uniquely determined by the quasi-complex structure, and
is the fundamental class of the manifold, or the orientation, uniquely determined by the quasi-complex structure, and 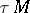 is the tangent bundle of
is the tangent bundle of 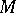 . If
. If  is taken to be a characteristic class with rational coefficients, then the corresponding Chern number will be rational. The Chern number
is taken to be a characteristic class with rational coefficients, then the corresponding Chern number will be rational. The Chern number 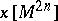 depends only on the homogeneous component of
depends only on the homogeneous component of  of degree
of degree 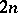 . The Chern numbers are quasi-complex bordism invariants, and hence the characteristic class
. The Chern numbers are quasi-complex bordism invariants, and hence the characteristic class  induces a homomorphism
induces a homomorphism 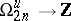 .
.
A partition of a number  is a set
is a set  of non-negative integers with
of non-negative integers with 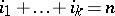 . If
. If 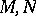 are two quasi-complex manifolds of dimension
are two quasi-complex manifolds of dimension 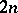 such that
such that 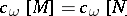 (cf. Chern class) for all partitions
(cf. Chern class) for all partitions 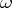 of
of  , then the manifolds
, then the manifolds 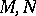 are cobordant (in the quasi-complex sense).
are cobordant (in the quasi-complex sense).
Let 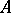 be a free Abelian group with basis
be a free Abelian group with basis 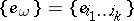 in one-to-one correspondence with the set of all partitions of
in one-to-one correspondence with the set of all partitions of  . The cited theorem asserts that the homomorphism
. The cited theorem asserts that the homomorphism
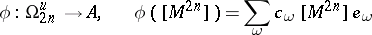 |
is a monomorphism. Below a description of the image of the homomorphism 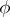 is given (the Milnor–Hirzebruch problem). In other words, which sets of integers
is given (the Milnor–Hirzebruch problem). In other words, which sets of integers  , defined for all partitions
, defined for all partitions 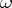 of a number
of a number  , arise as the Chern numbers of quasi-complex manifolds? A Chern number can be defined in an arbitrary multiplicative oriented cohomology theory
, arise as the Chern numbers of quasi-complex manifolds? A Chern number can be defined in an arbitrary multiplicative oriented cohomology theory 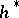 , except that in this case the Chern number of a quasi-complex manifold will be an element of the ring
, except that in this case the Chern number of a quasi-complex manifold will be an element of the ring 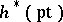 . Dual to the cohomology theory
. Dual to the cohomology theory 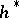 is a homology theory
is a homology theory  , and since
, and since 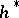 is oriented and multiplicative, there is for each quasi-complex manifold
is oriented and multiplicative, there is for each quasi-complex manifold 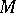 a unique fundamental class
a unique fundamental class 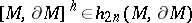 , where
, where 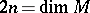 . Moreover, as in the ordinary theory there is a pairing
. Moreover, as in the ordinary theory there is a pairing
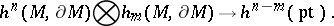 |
If 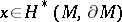 , then the application of
, then the application of  to
to 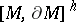 with respect to this pairing is denoted by
with respect to this pairing is denoted by 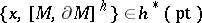 . For a characteristic class
. For a characteristic class 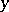 with values in
with values in 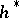 and a closed quasi-complex manifold
and a closed quasi-complex manifold 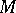 , the element
, the element 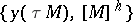 is called the Chern number in the theory
is called the Chern number in the theory 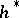 . The preceding considerations apply also to
. The preceding considerations apply also to 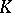 -theory. Let
-theory. Let  be a quasi-complex manifold (possibly with boundary), let
be a quasi-complex manifold (possibly with boundary), let 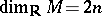 and let
and let  be an arbitrary element of
be an arbitrary element of 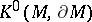 . Then the integer
. Then the integer
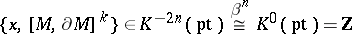 |
can be computed according to the formula
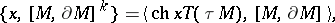 |
where 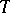 is the Todd class given by the series
is the Todd class given by the series  . If the manifold
. If the manifold  is closed, then putting
is closed, then putting 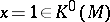 one obtains
one obtains 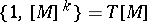 . The characteristic number
. The characteristic number 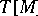 is called the Todd genus of the manifold
is called the Todd genus of the manifold  and is an integer for any quasi-complex manifold
and is an integer for any quasi-complex manifold 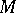 .
.  is often denoted by
is often denoted by 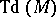 .
.
One of the most important examples of a quasi-complex manifold is a tangent manifold. Let 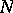 be a closed real manifold of dimension
be a closed real manifold of dimension  . The manifold
. The manifold 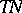 of all tangent vectors to
of all tangent vectors to 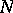 has a natural quasi-complex structure:
has a natural quasi-complex structure: 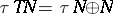 ,
, 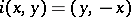 . Fix a Riemannian metric on
. Fix a Riemannian metric on 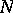 and let
and let 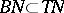 denote the manifold with boundary consisting of all vectors of length not exceeding one. If
denote the manifold with boundary consisting of all vectors of length not exceeding one. If 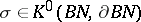 , then the integer
, then the integer 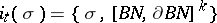 is called the topological index of the element
is called the topological index of the element 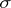 . If
. If 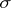 is the class of the symbol of an elliptic operator
is the class of the symbol of an elliptic operator 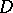 defined on
defined on 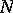 , then
, then 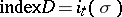 (the Atiyah–Singer theorem), and applying the above formula for computing the integer
(the Atiyah–Singer theorem), and applying the above formula for computing the integer 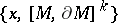 leads to the cohomological form of the index theorem.
leads to the cohomological form of the index theorem.
For a set 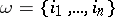 of non-negative integers and a closed quasi-complex manifold
of non-negative integers and a closed quasi-complex manifold 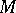 of dimension
of dimension 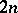 , let
, let  be the Chern number in
be the Chern number in 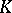 -theory:
-theory:
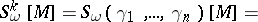 |
 |
and let 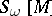 be the ordinary Chern number
be the ordinary Chern number  . The number
. The number 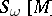 can be distinct from zero only if
can be distinct from zero only if 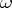 is a partition of
is a partition of  . The number
. The number 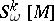 can be distinct from zero for sets
can be distinct from zero for sets  with
with 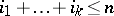 . Any homomorphisms
. Any homomorphisms 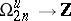 can be expressed as a linear combination with integer coefficients of homomorphisms
can be expressed as a linear combination with integer coefficients of homomorphisms 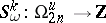 , with
, with 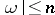 , where
, where 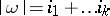 (the Stong–Hattori theorem). The characteristic numbers
(the Stong–Hattori theorem). The characteristic numbers  with
with  can be expressed in the form
can be expressed in the form
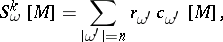 |
where 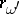 are rational coefficients and
are rational coefficients and 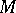 is any closed quasi-complex manifold of dimension
is any closed quasi-complex manifold of dimension  . Let
. Let  be an arbitrary element of the group
be an arbitrary element of the group 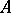 ,
,  and let
and let 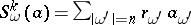 . Then the element
. Then the element 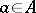 lies in the image of the homomorphism
lies in the image of the homomorphism 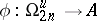 if and only if
if and only if  is an integer for all sets
is an integer for all sets 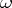 with
with 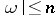 .
.
For references see Chern class.
Comments
Cf. Cobordism for the notions "quasi-complex manifold" and "complex-oriented cohomology theory" . Cf. also the comments to Chern class.
Chern number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chern_number&oldid=13675