Cheeger finiteness theorem
From Encyclopedia of Mathematics
A theorem stating that for given positive numbers  ,
, 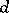 ,
,  ,
, 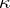 there exist only finitely many diffeomorphism classes of compact
there exist only finitely many diffeomorphism classes of compact  -dimensional Riemannian manifolds
-dimensional Riemannian manifolds 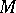 satisfying
satisfying
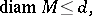 |
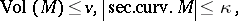 |
i.e. for every given sequence of compact  -dimensional Riemannian manifolds satisfying these bounds, there is an infinite subsequence for which any two of the manifolds are diffeomorphic.
-dimensional Riemannian manifolds satisfying these bounds, there is an infinite subsequence for which any two of the manifolds are diffeomorphic.
The proof is based on discretizations of Riemannian manifolds and on lower bounds for the injectivity radius (cf. Berger inequality) in terms of  ,
, 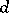 ,
,  ,
,  .
.
Cf. also Riemannian manifold.
References
| [a1] | I. Chavel, "Riemannian geometry: A modern introduction" , Cambridge Univ. Press (1995) |
| [a2] | J. Cheeger, "Finiteness theorems in Riemannian manifolds" Amer. J. Math. , 92 (1970) pp. 61–74 |
How to Cite This Entry:
Cheeger finiteness theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cheeger_finiteness_theorem&oldid=17305
Cheeger finiteness theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cheeger_finiteness_theorem&oldid=17305
This article was adapted from an original article by H. Kaul (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article