Chebyshev theorems on prime numbers
The theorems 1)–8) on the distribution of prime numbers, proved by P.L. Chebyshev [1] in 1848–1850.
Let  be the number of primes not exceeding
be the number of primes not exceeding  , let
, let  be an integer
be an integer  , let
, let  be a prime number, let
be a prime number, let  be the natural logarithm of
be the natural logarithm of  , and let
, and let
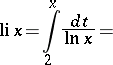 | (*) |
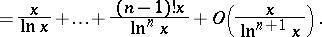 |
1) For any  the sum of the series
the sum of the series
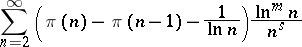 |
has a finite limit as 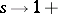 .
.
2) For arbitrary small  and arbitrary large
and arbitrary large  , the function
, the function  satisfies the two inequalities
satisfies the two inequalities
 |
infinitely often.
3) The fraction 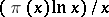 cannot have a limit distinct from 1 as
cannot have a limit distinct from 1 as 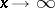 .
.
4) If 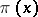 can be expressed algebraically in
can be expressed algebraically in  ,
, 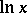 and
and 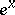 up to order
up to order 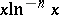 , then the expression must be (*). After this, Chebyshev introduced two new distribution functions for prime numbers — the Chebyshev functions (cf. Chebyshev function)
, then the expression must be (*). After this, Chebyshev introduced two new distribution functions for prime numbers — the Chebyshev functions (cf. Chebyshev function)
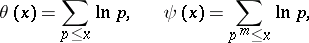 |
and actually determined the order of growth of these functions. Hence he was the first to obtain the order of growth of 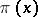 and of the
and of the  -th prime number
-th prime number  . More precisely, he proved:
. More precisely, he proved:
5) If 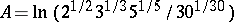 , then for
, then for 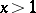 the inequalities
the inequalities
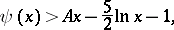 |
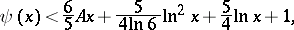 |
hold.
6) For  larger than some
larger than some  , the inequality
, the inequality
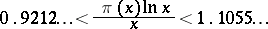 |
holds.
7) There exist constants  such that for all
such that for all  the
the  -th prime number
-th prime number  satisfies the inequalities
satisfies the inequalities
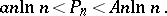 |
8) For  there is at least one prime number in the interval
there is at least one prime number in the interval  (Bertrand's postulate).
(Bertrand's postulate).
The main idea of the method of proof of 1)–4) lies in the study of the behaviour of the quantities
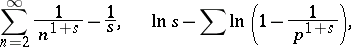 |
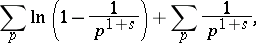 |
and their derivatives as 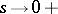 . The basis of the method of deducing 5)–8) is the Chebyshev identity:
. The basis of the method of deducing 5)–8) is the Chebyshev identity:
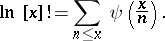 |
References
| [1] | P.L. Chebyshev, "Oeuvres de P.L. Tchebycheff" , 1–2 , Chelsea (1961) (Translated from Russian) |
Comments
By now (1987) Chebyshev's theorems have been superceded by better results. E.g.,
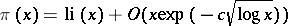 |
(see [a1] for even better results); further 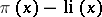 changes sign infinitely often. More results, as well as references, can be found in [a1], Chapt. 12, Notes.
changes sign infinitely often. More results, as well as references, can be found in [a1], Chapt. 12, Notes.
References
| [a1] | A. Ivic, "The Riemann zeta-function" , Wiley (1985) |
Chebyshev theorems on prime numbers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chebyshev_theorems_on_prime_numbers&oldid=16234