Chebyshev quadrature formula
An interpolation quadrature formula with equal coefficients:
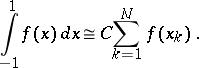 | (*) |
The weight function is equal to one, and the integration interval is finite and is taken to coincide with 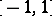 . The number of parameters defining the quadrature formula (*) is
. The number of parameters defining the quadrature formula (*) is 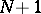 (
(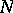 nodes and the value of the coefficient
nodes and the value of the coefficient 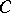 ). The parameters are determined by the requirement that (*) is exact for all polynomials of degree
). The parameters are determined by the requirement that (*) is exact for all polynomials of degree 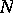 or less, or equivalently, for the monomials
or less, or equivalently, for the monomials 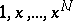 . The parameter
. The parameter 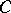 is obtained from the condition that the quadrature formula is exact for
is obtained from the condition that the quadrature formula is exact for 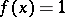 , and is equal to
, and is equal to 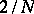 . The nodes
. The nodes 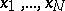 turn out to be real only for
turn out to be real only for 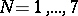 and
and 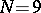 . For
. For 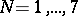 the nodes were calculated by P.L. Chebyshev. For
the nodes were calculated by P.L. Chebyshev. For 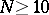 among the nodes of the Chebyshev quadrature formula there always are complex ones (cf. [1]). The algebraic degree of precision of the Chebyshev quadrature formula is
among the nodes of the Chebyshev quadrature formula there always are complex ones (cf. [1]). The algebraic degree of precision of the Chebyshev quadrature formula is 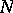 for odd
for odd 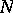 and
and 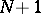 for even
for even 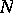 . Formula (*) was proposed by Chebyshev in 1873.
. Formula (*) was proposed by Chebyshev in 1873.
References
| [1] | N.M. Krylov, "Approximate calculation of integrals" , Macmillan (1962) (Translated from Russian) |
Comments
This formula is to be distinguished from the Gauss–Chebyshev quadrature formula (cf. Gauss quadrature formula), which is defined using a weight function 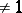 .
.
The original reference for Chebyshev's quadrature formula is [a3]. S.N. Bernshtein [a2] has shown that the nodes are real only if 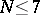 or
or 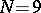 . A detailed discussion of the formula can be found in [a4]. Tables of quadrature nodes are given in [a1].
. A detailed discussion of the formula can be found in [a4]. Tables of quadrature nodes are given in [a1].
References
| [a1] | A. Segun, M. Abramowitz, "Handbook of mathematical functions" , Appl. Math. Ser. , 55 , Nat. Bur. Standards (1970) |
| [a2] | S.N. Bernshtein, "Sur les formules quadratures de Cotes et Chebyshev" C.R. Acad. Sci. USSR , 14 pp. 323–326 |
| [a3] | P.L. Chebyshev, "Sur les quadratures" J. Math. Pures Appl. , 19 : 2 (1874) pp. 19–34 (Oeuvres, Vol. 2, pp. 165–180) |
| [a4] | F.B. Hildebrand, "Introduction to numerical analysis" , McGraw-Hill (1974) |
| [a5] | P.J. Davis, P. Rabinowitz, "Methods of numerical integration" , Acad. Press (1984) |
Chebyshev quadrature formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chebyshev_quadrature_formula&oldid=16279