Chebyshev function
From Encyclopedia of Mathematics
One of the two functions, of a positive argument  , defined as follows:
, defined as follows:
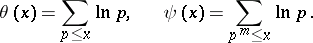 |
The first sum is taken over all prime numbers 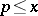 , and the second over all positive integer powers
, and the second over all positive integer powers 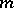 of prime numbers
of prime numbers 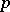 such that
such that 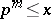 . The function
. The function  can be expressed in terms of the Mangoldt function
can be expressed in terms of the Mangoldt function
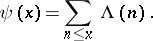 |
It follows from the definitions of 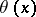 and
and 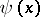 that
that 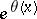 is equal to the product of all prime numbers
is equal to the product of all prime numbers  , and that the quantity
, and that the quantity 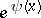 is equal to the least common multiple of all positive integers
is equal to the least common multiple of all positive integers 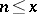 . The functions
. The functions 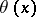 and
and 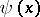 are related by the identity
are related by the identity
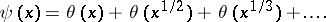 |
These functions are also closely connected with the function
 |
which expresses the number of the prime numbers  .
.
References
| [1] | P.L. Chebyshev, "Mémoire sur les nombres premiers" J. Math. Pures Appl. , 17 (1852) pp. 366–390 (Oeuvres, Vol. 1, pp. 51–70) |
Comments
For properties of the Chebyshev functions 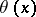 and
and 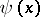 see [a1], Chapt. 12.
see [a1], Chapt. 12.
References
| [a1] | A. Ivic, "The Riemann zeta-function" , Wiley (1985) |
How to Cite This Entry:
Chebyshev function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chebyshev_function&oldid=12881
Chebyshev function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chebyshev_function&oldid=12881
This article was adapted from an original article by S.A. Stepanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article