Characteristic of a field
From Encyclopedia of Mathematics
A positive prime number or the number 0 that is uniquely determined for a given field in the following way. If for some 
,
 |
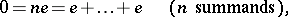where 
is the unit element of the field 
, then the smallest such 
is a prime number; it is called the characteristic of 
. If there are no such numbers, then one says that the characteristic of 
is zero or that 
is a field of characteristic zero. Sometimes such a field is said to be without characteristic or of characteristic infinity 
. Every field of characteristic zero contains a subfield isomorphic to the field of all rational numbers, and a field of finite characteristic 
contains a subfield isomorphic to the field of residue classes modulo 
.
How to Cite This Entry:
Characteristic of a field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Characteristic_of_a_field&oldid=17329
Characteristic of a field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Characteristic_of_a_field&oldid=17329
This article was adapted from an original article by O.A. Ivanova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article