Characteristic functional
An analogue of the concept of a characteristic function; it is used in the infinite-dimensional case. Let 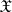 be a non-empty set, let
be a non-empty set, let 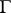 be a vector space of real-valued functions defined on
be a vector space of real-valued functions defined on 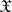 and let
and let 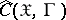 be the smallest
be the smallest 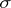 -algebra of subsets of
-algebra of subsets of 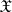 relative to which all functions in
relative to which all functions in  are measurable. The characteristic functional of a probability measure
are measurable. The characteristic functional of a probability measure 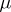 given on
given on 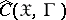 is defined as the complex-valued functional
is defined as the complex-valued functional 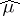 on
on 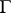 given by the equation
given by the equation
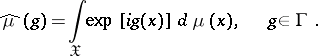 |
From now on the most important and simplest case when  is a separable real Banach space and
is a separable real Banach space and 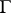 is its topological dual
is its topological dual 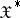 is studied. In this case
is studied. In this case  coincides with the
coincides with the 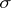 -algebra of Borel sets of
-algebra of Borel sets of 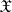 . The concept of a characteristic functional for infinite-dimensional Banach spaces was introduced by A.N. Kolmogorov in [1].
. The concept of a characteristic functional for infinite-dimensional Banach spaces was introduced by A.N. Kolmogorov in [1].
The characteristic functional of a random variable 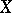 with values in
with values in 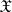 is, by definition, that of its probability distribution
is, by definition, that of its probability distribution 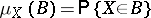 ,
, 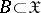 .
.
Main properties of the characteristic functional:
1) 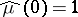 and
and 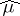 is positive definite, i.e.
is positive definite, i.e. 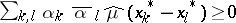 for any finite set of complex numbers
for any finite set of complex numbers  and elements
and elements 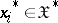 ;
;
2) 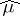 is continuous in the strong topology and sequentially continuous in the weak
is continuous in the strong topology and sequentially continuous in the weak  topology of
topology of 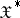 ;
;
3) 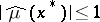 ,
,
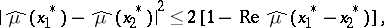 |
where 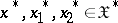 ;
;
4) 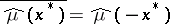 ; in particular,
; in particular, 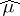 takes only real values (and is an even functional) if and only if the measure
takes only real values (and is an even functional) if and only if the measure 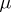 is symmetric, that is,
is symmetric, that is, 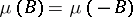 , where
, where  ;
;
5) the characteristic functional determines the measure uniquely;
6) the characteristic functional of the convolution of two probability measures (of the sum of two independent random variables) is the product of their characteristic functionals.
In the finite-dimensional case the method of characteristic functionals is based on the theorem about the continuity of the correspondence between measures and their characteristic functionals, and on a theorem concerning the description of the class of characteristic functionals. In the infinite-dimensional case the direct analogues of these theorems do not hold. If a sequence of probability measures 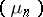 converges weakly to
converges weakly to 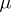 , then
, then 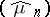 converges pointwise to
converges pointwise to 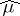 , and this convergence is uniform on bounded subsets of
, and this convergence is uniform on bounded subsets of 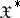 ; if
; if 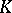 is a weakly relatively-compact family of probability measures on
is a weakly relatively-compact family of probability measures on  , then the family
, then the family 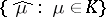 is equicontinuous in the strong topology of
is equicontinuous in the strong topology of 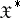 . The converse assertions only hold in the finite-dimensional case. However, the conditions of convergence and of weak relative compactness of families of probability measures can be expressed in terms of characteristic functionals (see [2]). Furthermore, in contrast to the finite-dimensional case, not every positive-definite normalized (equal to 1 at the origin) continuous functional is a characteristic functional: continuity in the metric topology is not sufficient. A topology in
. The converse assertions only hold in the finite-dimensional case. However, the conditions of convergence and of weak relative compactness of families of probability measures can be expressed in terms of characteristic functionals (see [2]). Furthermore, in contrast to the finite-dimensional case, not every positive-definite normalized (equal to 1 at the origin) continuous functional is a characteristic functional: continuity in the metric topology is not sufficient. A topology in 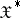 is called sufficient, or necessary, if in this topology the continuity of a positive-definite normalized functional is sufficient, or necessary, for it to be the characteristic functional of some probability measure on
is called sufficient, or necessary, if in this topology the continuity of a positive-definite normalized functional is sufficient, or necessary, for it to be the characteristic functional of some probability measure on 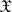 . A necessary and sufficient topology is said to be an
. A necessary and sufficient topology is said to be an 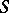 -topology. A space
-topology. A space 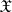 is called an
is called an 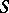 -space if there is an
-space if there is an 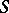 -topology on
-topology on 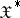 . A Hilbert space is an
. A Hilbert space is an 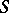 -space (see [3]).
-space (see [3]).
The most important characteristic functionals are those of Gaussian measures. A measure 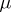 in
in 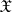 is called a centred Gaussian measure if for all
is called a centred Gaussian measure if for all 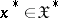 ,
,
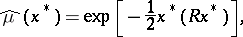 | (*) |
where 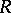 , a bounded linear positive operator from
, a bounded linear positive operator from 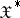 into
into  , is the covariance operator of the measure
, is the covariance operator of the measure 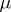 , defined by the relation
, defined by the relation
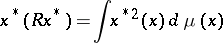 |
(see [4]). In contrast to the finite-dimensional case, not every functional of the form (*) is a characteristic functional: additional restrictions on 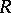 are needed, depending on the space
are needed, depending on the space 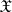 . For example, if
. For example, if 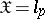 ,
, 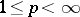 , then an additional (necessary and sufficient) condition is
, then an additional (necessary and sufficient) condition is 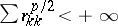 , where
, where 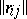 is the matrix of the operator
is the matrix of the operator 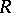 in the natural basis (see [5]). In particular, in a Hilbert space the additional condition is that the operator
in the natural basis (see [5]). In particular, in a Hilbert space the additional condition is that the operator 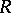 be nuclear.
be nuclear.
References
| [1] | A.N. Kolmogorov, C.R. Acad. Sci. Paris , 200 (1935) pp. 1717–1718 |
| [2] | Yu.V. Prokhorov, "Convergence of random processes and limit theorems in probability theory" Theory Probab. Appl. , 1 (1956) pp. 157–214 Teor. Veroyatnost. i Primen. , 1 : 2 (1956) pp. 177–238 |
| [3] | V.V. Sazonov, "A remark on characteristic functionals" Theory Probab. Appl. , 3 (1958) pp. 188–192 Teor. Veroyatnost. i Primen. , 3 : 2 (1958) pp. 201–205 |
| [4] | N.N. Vakhania, V.I. Tarieladze, S.A. Chobanyan, "Probability distributions on Banach spaces" , Reidel (1987) (Translated from Russian) |
| [5] | N.N. Vakhania, "Sur les répartitions de probabilités dans les espaces de suites numériques" C.R. Acad. Sci. Paris , 260 (1965) pp. 1560–1562 |
Comments
References
| [a1] | N.N. Vakhania, "Probability distributions on linear spaces" , North-Holland (1981) (Translated from Russian) |
Characteristic functional. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Characteristic_functional&oldid=11837