Characteristic
One of the basic concepts in the theory of partial differential equations. The role of characteristics manifests itself in essential properties of these equations such as the local properties of solutions, the solvability of various problems, their being well posed, etc.
Suppose that
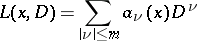 |
is a linear partial differential operator of order 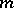 , and let
, and let
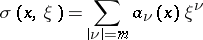 |
be its symbol. Here 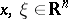 ,
, 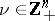 is a multi-index,
is a multi-index, 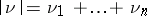 ,
, 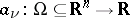 ,
,
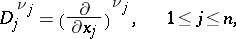 |
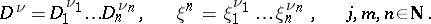 |
Let 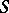 be the hypersurface defined in
be the hypersurface defined in 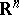 by the equation
by the equation 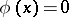 , where
, where 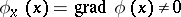 for
for 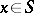 , and let
, and let
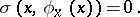 | (1) |
In this case 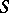 is called a characteristic surface or a characteristic for the operator
is called a characteristic surface or a characteristic for the operator  . Other names are: characteristic manifold, characteristic line (in case
. Other names are: characteristic manifold, characteristic line (in case 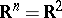 ).
).
The example of the Cauchy problem is discussed below. Let 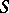 be the arbitrary (not necessarily characteristic) hypersurface in
be the arbitrary (not necessarily characteristic) hypersurface in 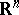 defined by the relations
defined by the relations
 |
Let 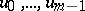 be functions defined on
be functions defined on 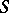 in a neighbourhood
in a neighbourhood 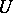 of
of 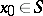 , and let
, and let
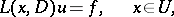 |
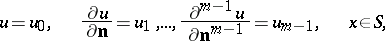 |
be the Cauchy problem for the unknown function  . Here
. Here  is a given function,
is a given function, 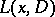 is a given linear differential operator of order
is a given linear differential operator of order 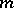 , and
, and 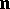 is a vector orthonormal to
is a vector orthonormal to 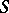 . Assume, to be definite, that
. Assume, to be definite, that 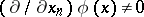 ,
, 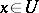 . Then, by the change of variables
. Then, by the change of variables
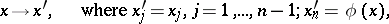 |
one arrives at the equation
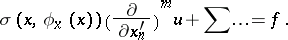 | (2) |
The expression under the sign 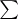 that is not written out does not contain partial derivatives of
that is not written out does not contain partial derivatives of  with respect to
with respect to 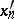 of order
of order 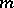 . Two cases arise:
. Two cases arise:
1) 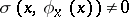 ,
, 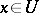 ;
;
2) 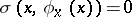 ,
, 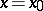 .
.
In the first case division of (2) by 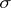 leads to an equation that can be solved for the highest partial derivative of
leads to an equation that can be solved for the highest partial derivative of 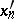 , that is, can be written in normal form. The initial conditions can be put in the form
, that is, can be written in normal form. The initial conditions can be put in the form
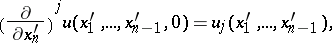 |
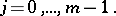 |
For this case the Cauchy problem has been well studied. For example, when the functions 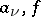 in the equations and when the initial data
in the equations and when the initial data 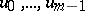 are real-analytic, there exists a unique solution of this problem in the class of real-analytic functions in a sufficiently small neighbourhood of
are real-analytic, there exists a unique solution of this problem in the class of real-analytic functions in a sufficiently small neighbourhood of 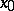 (the Cauchy–Kovalevskaya theorem). In the second case
(the Cauchy–Kovalevskaya theorem). In the second case 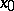 is a characteristic point, and if (1) holds for all
is a characteristic point, and if (1) holds for all 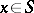 , then
, then 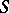 is called a characteristic. In this case (2) implies that the initial data cannot be arbitrary, and the study of the Cauchy problem becomes complicated.
is called a characteristic. In this case (2) implies that the initial data cannot be arbitrary, and the study of the Cauchy problem becomes complicated.
For example, for the equation
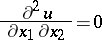 | (3) |
initial data can be given on one of its characteristics  :
:
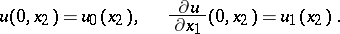 | (4) |
If the function 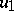 is not constant, then the Cauchy problem (3), (4) has no solution in the space
is not constant, then the Cauchy problem (3), (4) has no solution in the space 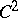 . But if
. But if 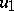 is constant, for example equal to
is constant, for example equal to 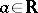 , then a solution is not unique in
, then a solution is not unique in 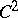 , since it may be any function of the form
, since it may be any function of the form
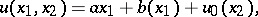 |
where
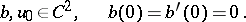 |
Thus, the Cauchy problem differs substantially, depending on whether the initial data are given on a characteristic surface or not.
A characteristic has the property of invariance under invertible transformations of the independent variables: If 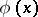 is a solution of (1) and if the transformation
is a solution of (1) and if the transformation 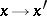 leads to
leads to 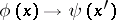 ,
, 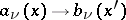 , then
, then 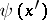 satisfies the equation
satisfies the equation
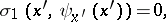 |
where
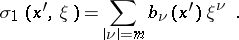 |
Another property of a characteristic is that 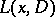 is, relative to a characteristic
is, relative to a characteristic 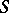 , an interior differential operator.
, an interior differential operator.
Elliptic linear differential operators are defined as operators for which there are no (real) characteristics. The definitions of hyperbolic and parabolic operators are also closely connected with the concept of a characteristic. For example, a second-order differential operator in two variables (i.e. 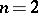 ) is of hyperbolic type if it has two families of characteristics and of parabolic type if it has one such family. The knowledge of the characteristics of a differential equation makes it possible to reduce the equation to simpler form. For example, let the equation
) is of hyperbolic type if it has two families of characteristics and of parabolic type if it has one such family. The knowledge of the characteristics of a differential equation makes it possible to reduce the equation to simpler form. For example, let the equation
 | (5) |
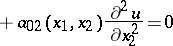 |
be hyperbolic. That is, equation (1), which now reads
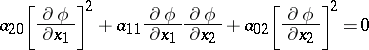 |
determines two distinct families of characteristics:
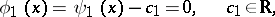 |
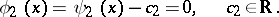 |
For any selected pair 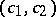 the change of variables
the change of variables 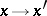 by the formula
by the formula
 |
transforms (5) to the canonical form
 |
For a non-linear differential equation
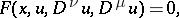 | (6) |
where 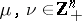 are multi-indices and
are multi-indices and  ,
, 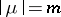 , the characteristic
, the characteristic 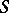 is defined as the hypersurface in
is defined as the hypersurface in 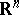 with the equation
with the equation 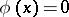 , where
, where 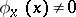 and
and 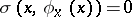 for
for 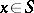 . In this case the symbol for the operator (6) given by the function
. In this case the symbol for the operator (6) given by the function 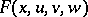 is defined as follows:
is defined as follows:
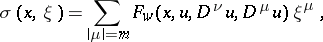 |
with the usual assumption 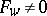 . Evidently,
. Evidently, 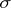 may depend, apart from the variables
may depend, apart from the variables  and
and 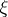 , also on
, also on  , and
, and 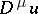 . Suppose, for example, that a first-order equation is given
. Suppose, for example, that a first-order equation is given 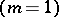 . For simplicity, suppose in addition that
. For simplicity, suppose in addition that 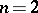 . Then (6) takes the form
. Then (6) takes the form
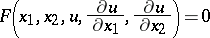 |
with a function 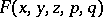 . The equation of the characteristics is:
. The equation of the characteristics is:
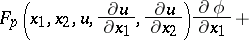 |
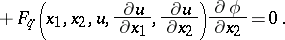 |
Since a solution 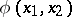 of this equation may, in fact, depend on
of this equation may, in fact, depend on 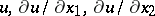 , it can be given in parametric form
, it can be given in parametric form
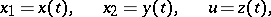 |
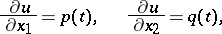 |
where these functions satisfy the ordinary differential equations
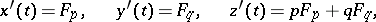 |
 |
Geometrically the  -tuple
-tuple 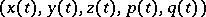 determines the so-called characteristic strip (for
determines the so-called characteristic strip (for 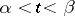 ). The projection of this strip onto the space
). The projection of this strip onto the space 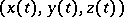 determines a curve in
determines a curve in 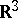 such that at every point of it, it touches the plane with direction coefficients
such that at every point of it, it touches the plane with direction coefficients 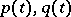 . This curve is also called a characteristic of the equation (6).
. This curve is also called a characteristic of the equation (6).
References
| [1] | S. Misohata, "The theory of partial differential equations" , Cambridge Univ. Press (1973) |
| [2] | E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 2. Partielle Differentialgleichungen erster Ordnung für die gesuchte Funktion , Akad. Verlagsgesell. (1944) |
| [3] | P. Hartman, "Ordinary differential equations" , Birkhäuser (1982) |
| [4] | I.G. Petrovskii, "Partial differential equations" , Saunders (1967) (Translated from Russian) |
| [5] | N.S. Koshlyakov, E.B. Gliner, M.M. Smirnov, "Partial differential equations" , Moscow (1970) (In Russian) |
| [6] | V.S. Vladimirov, "Die Gleichungen der mathematischen Physik" , MIR (1984) (Translated from Russian) |
| [7] | S.G. Mikhlin, "A course of mathematical physics" , Moscow (1968) (In Russian) |
| [8] | A.N. [A.N. Tikhonov] Tichonoff, A.A. Samarskii, "Differentialgleichungen der mathematischen Physik" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
Comments
It has to be stressed that for first-order partial differential equations that are non-linear with respect to 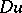 there is a whole family of characteristics through a given point (a conoid). A classic notion in this connection is the one of Monge cones (cf. also Monge cone). Referring again to the case
there is a whole family of characteristics through a given point (a conoid). A classic notion in this connection is the one of Monge cones (cf. also Monge cone). Referring again to the case 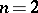 , the normal vectors to possible integral surfaces
, the normal vectors to possible integral surfaces 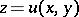 through a given point
through a given point 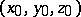 are defined by the equation
are defined by the equation 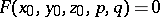 . The envelope of the associated one-parameter family of tangent planes
. The envelope of the associated one-parameter family of tangent planes 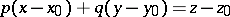 , i.e. the set of characteristic directions
, i.e. the set of characteristic directions 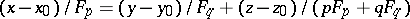 , is called the Monge cone at the point
, is called the Monge cone at the point 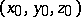 .
.
References
| [a1] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 1–2 , Interscience (1953–1962) (Translated from German) |
| [a2] | P.R. Garabedian, "Partial differential equations" , Wiley (1964) |
| [a3] | L.V. Hörmander, "The analysis of linear partial differential operators" , 1–4 , Springer (1983–1985) |
| [a4] | F. John, "Partial differential equations" , Springer (1974) |
| [a5] | A. Jeffrey, "Quasilinear hyperbolic systems and waves" , Pitman (1976) |
| [a6] | E. Cartan, "Les systèmes différentielles extérieurs et leur applications géométriques" , Hermann (1945) |
| [a7] | I.G. Petrovskii, "Lectures on partial differential equations" , Interscience (1954) (Translated from Russian) |
Characteristic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Characteristic&oldid=18652