Character of a finite-dimensional representation of a semi-simple Lie algebra

The function that assigns to every weight of the representation the dimension of the corresponding weight subspace. If 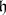is a Cartan subalgebra of a semi-simple Lie algebra 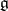over an algebraically closed field 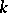of characteristic , 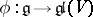is a linear representation and 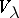is the weight subspace corresponding to 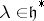, then the character of the representation 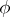(or of the 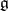-module 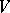) can be written in the form

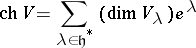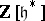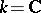and can be regarded as an element of the group ring . If and 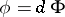, where 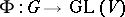is an analytic linear representation of a Lie group 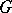with Lie algebra 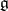, then 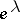can be regarded as the function on 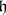suggested by the notation and 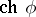coincides with the function 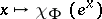(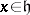), where 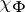is the character of the representation 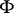. Characters of a representation of a Lie algebra have the following properties:

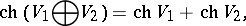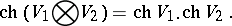References

[1]	J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French)
[2]	J. Dixmier, "Algèbres enveloppantes" , Gauthier-Villars (1974)