Channel with multiple directions

multi-terminal channel, multi-user channel

A communication channel for which it is possible to transmit information in several directions simultaneously. The description which follows is for a memoryless discrete-time multi-user channel with finite input and output alphabets. Let be finite sets, where (the alphabet) 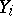is the set of possible signals which the 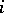-th transmitter can send, and let be finite sets, where (the alphabet) 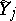is the set of possible signals which the 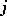-th receiver can receive. Suppose further that a stochastic matrix

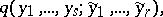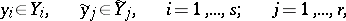is given. Two sets of random vectors 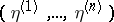and 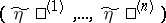, where 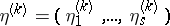, , 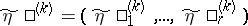defined on some probability space 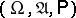, are said to be connected by a segment of length of a homogeneous multi-user channel with inputs and outputs if 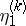and 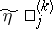, (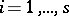; ; 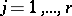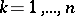), take values in the sets 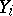and 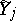, respectively, and the formula

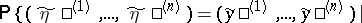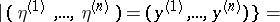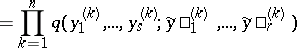holds for any 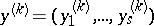and , , , , ; .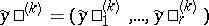

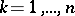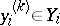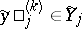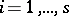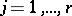The intuitive interpretation is that each input and each output of a multi-user channel is situated in a different terminal (end), i.e. there are 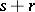terminals in total. This means that a transmitter or receiver situated in some terminal cannot use information known to the transmitters or the receivers of other terminals. Multi-user channels possessing this property are often called pure channels, in contrast to mixed multi-user channels, for which there exist terminals containing simultaneously several inputs and outputs of the channel. The complexity of the analysis of mixed multi-user channels is due to the fact that the transmitters of some terminal can, in selecting the next signal to be transmitted, use the information obtained at that moment by all the receivers of the given terminal; the receivers of this terminal can in turn use all the information available in the terminal at the given moment.

The most general problem in information transmission along a pure memoryless multi-user channel, as intuitively described above, is the following. Suppose that there are 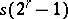discrete stationary sources of information 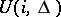(cf. Information, source of); 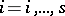, , 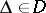where 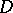is the set of all non-empty subsets of the index set 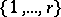generating the messages 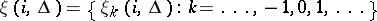, where the individual components of the message 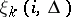take values in some set 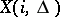of volume 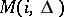; 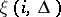can be required as the message intended for transmission from the 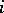-th input of the channel to all outputs with indices 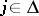. The message at the 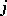-th output, 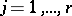, is a set of random processes 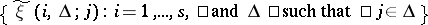, where

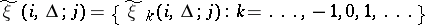and the components 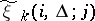take values in 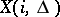. Let segments of messages

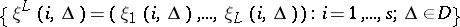of length 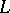be transmitted using a segment of length 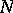of a memoryless multi-user channel using the following block methods of (en)coding and decoding. The (en)coding is determined by a set of (en)coding mappings 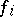such that

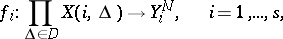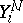( being the direct product of copies of 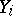), and the decoding by a set of decoding mappings:

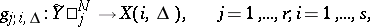and 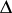is such that .

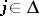The set of (en)coding functions 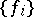establishes a functional dependence between the segments of length 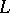of the messages of all possible sources and the segments of length 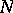of the signals at the inputs of the channel. The set of decoding functions 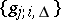establishes a functional dependence between the segments of length 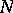of the signals at the outputs of the channel and the segments of length 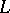of the messages generated at each output. 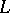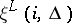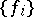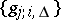If the joint distribution of the segments of length of the messages, , the (en)coding and decoding functions and , and the transition probabilities of the memoryless multi-user channel are known, then one can calculate the error probability 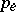, defined by the formula .

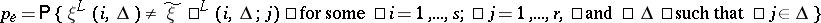A set 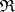of sets (vectors) of rates 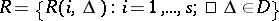in the 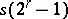-dimensional Euclidean space is called the capacity region of the channel considered here if for any 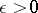there exist an integer 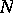, (en)codings 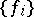and decodings 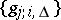such that

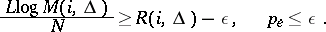The problem of describing the region 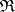is one of the main problems in the theory of multi-user channels. In the general case this problem is unsolved. A final solution of it has been obtained only in certain special cases, for example, for multiple-access channels (that is, a multi-user channel with 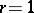) and for a certain class of broadcast channels (that is, channels with ).

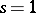References

[1]	C. Shannon, "Papers on information theory and cybernetics" , Moscow (1963) (In Russian; translated from English)
[2]	E.C. van der Meulen, "Advances in multi-user communication channels" , Proc. 1975 IEEE-USSR Joint Workshop Inform. Theory (Moscow, 15–19 Dec. 1975) , IEEE (1976) pp. 227–247
[3]	T.M. Cover, "Broadcast channels" IEEE Trans. Inform. Theory , 18 : 1 (1972) pp. 2–14
[4]	D. Slepian, J.K. Wolf, "A coding theorem for multiple access channels with correlated sources" Bell System Techn. J. , 52 : 7 (1973) pp. 1037–1076
[5]	I. Csiszar, J. Körner, "Information theory. Coding theorems for discrete memoryless systems" , Akad. Kiado (1981)