Centre manifold
Consider an autonomous system of ordinary differential equations
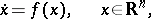 | (a1) |
where 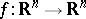 is sufficiently smooth,
is sufficiently smooth, 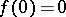 . Let the eigenvalues of the Jacobi matrix
. Let the eigenvalues of the Jacobi matrix 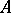 evaluated at the equilibrium position
evaluated at the equilibrium position  be
be 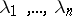 . Suppose the equilibrium is non-hyperbolic, i.e. has eigenvalues with zero real part. Assume also that there are
. Suppose the equilibrium is non-hyperbolic, i.e. has eigenvalues with zero real part. Assume also that there are 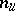 eigenvalues (counting multiplicities) with
eigenvalues (counting multiplicities) with 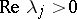 ,
, 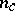 eigenvalues with
eigenvalues with  , and
, and 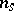 eigenvalues with
eigenvalues with 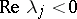 . Let
. Let 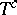 denote the linear (generalized) eigenspace of
denote the linear (generalized) eigenspace of 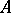 corresponding to the union of the
corresponding to the union of the 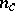 eigenvalues on the imaginary axis. The eigenvalues with
eigenvalues on the imaginary axis. The eigenvalues with 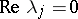 are often called critical, as is the eigenspace
are often called critical, as is the eigenspace 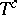 . Let
. Let 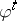 denote the flow (continuous-time dynamical system) associated with (a1). Under the assumptions stated above, the following centre manifold theorem holds [a7], [a9], [a3], [a11]: There is a locally defined smooth
denote the flow (continuous-time dynamical system) associated with (a1). Under the assumptions stated above, the following centre manifold theorem holds [a7], [a9], [a3], [a11]: There is a locally defined smooth 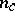 -dimensional invariant manifold
-dimensional invariant manifold 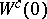 of
of 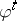 that is tangent to
that is tangent to 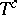 at
at  .
.
The manifold  is called the centre manifold. The centre manifold
is called the centre manifold. The centre manifold 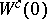 need not be unique. If
need not be unique. If 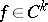 with finite
with finite 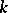 ,
, 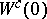 is a
is a 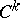 -manifold in some neighbourhood
-manifold in some neighbourhood 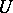 of
of 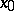 . However, as
. However, as 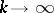 the neighbourhood
the neighbourhood 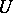 may shrink, thus resulting in the non-existence of a
may shrink, thus resulting in the non-existence of a 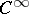 -manifold
-manifold 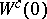 for certain
for certain 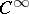 systems.
systems.
In a basis formed by all (generalized) eigenvectors of 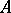 (or their linear combinations if the corresponding eigenvalues are complex), the system (a1) can be written as
(or their linear combinations if the corresponding eigenvalues are complex), the system (a1) can be written as
 | (a2) |
where 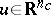 ,
, 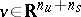 ,
, 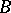 is an
is an  -matrix with all its
-matrix with all its 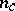 eigenvalues on the imaginary axis, while
eigenvalues on the imaginary axis, while 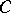 is an
is an 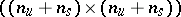 -matrix with no eigenvalue on the imaginary axis;
-matrix with no eigenvalue on the imaginary axis; 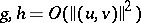 . A centre manifold
. A centre manifold 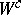 of (a2) can be locally represented as the graph of a smooth function
of (a2) can be locally represented as the graph of a smooth function 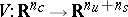 ,
, 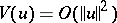 :
:
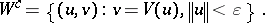 |
The following reduction principle is valid (see [a1], [a8]): The system (a2) is locally topologically equivalent (cf. Equivalence of dynamical systems) near the origin to the system
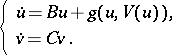 | (a3) |
The equations for  and
and  are uncoupled in (a3). The first equation is the restriction of (a2) to its centre manifold. Thus, the dynamics of (a2) near a non-hyperbolic equilibrium are determined by this restriction, since the second equation in (a3) is linear and has exponentially decaying/growing solutions. For example, if
are uncoupled in (a3). The first equation is the restriction of (a2) to its centre manifold. Thus, the dynamics of (a2) near a non-hyperbolic equilibrium are determined by this restriction, since the second equation in (a3) is linear and has exponentially decaying/growing solutions. For example, if 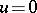 is the asymptotically stable equilibrium of the restriction and the matrix
is the asymptotically stable equilibrium of the restriction and the matrix 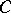 has no eigenvalue with positive real part, then
has no eigenvalue with positive real part, then 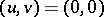 is the asymptotically stable equilibrium of (a2). If there is more than one centre manifold, then all the resulting systems (a3) with different
is the asymptotically stable equilibrium of (a2). If there is more than one centre manifold, then all the resulting systems (a3) with different 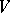 are locally topologically equivalent (actually, the
are locally topologically equivalent (actually, the 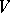 differ only by flat functions).
differ only by flat functions).
The second equation in (a3) can be replaced by the standard saddle:
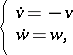 | (a4) |
with 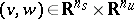 . In other words, near a non-hyperbolic equilibrium the system is locally topologically equivalent to the suspension of its restriction to the centre manifold by the standard saddle.
. In other words, near a non-hyperbolic equilibrium the system is locally topologically equivalent to the suspension of its restriction to the centre manifold by the standard saddle.
Consider now a system that depends smoothly on parameters:
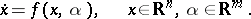 | (a5) |
Suppose that at 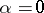 the system has a non-hyperbolic equilibrium
the system has a non-hyperbolic equilibrium 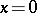 with
with 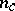 eigenvalues on the imaginary axis and
eigenvalues on the imaginary axis and 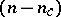 eigenvalues with non-zero real part. Let
eigenvalues with non-zero real part. Let 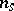 of them have negative real part, while
of them have negative real part, while 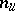 have positive real part. Applying the centre manifold theorem to the following extended system:
have positive real part. Applying the centre manifold theorem to the following extended system:
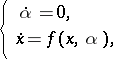 | (a6) |
one can prove the existence of a parameter-dependent local invariant manifold 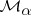 in (a5). The manifold has dimension
in (a5). The manifold has dimension 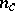 and
and 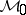 coincides with a centre manifold
coincides with a centre manifold 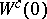 of the (a5) at
of the (a5) at 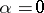 . Often, the manifold
. Often, the manifold 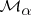 is called the centre manifold for all
is called the centre manifold for all 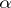 . For each small
. For each small 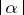 one can restrict system (a5) to
one can restrict system (a5) to 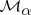 . Introducing a coordinate system on
. Introducing a coordinate system on 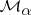 with
with 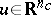 as the coordinate, this restriction will be represented by a smooth system:
as the coordinate, this restriction will be represented by a smooth system:
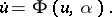 | (a7) |
At 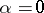 , the system (a7) is equivalent to the restriction of (a5) to its centre manifold
, the system (a7) is equivalent to the restriction of (a5) to its centre manifold 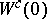 . The following results are known as the Šošitaišvili theorem [a10] (see also [a1], [a2], [a8]): The system (a5) is locally topologically equivalent near the origin to the suspension of (a7) by the standard saddle (a4). Moreover, (a7) can be replaced by any locally topologically equivalent system.
. The following results are known as the Šošitaišvili theorem [a10] (see also [a1], [a2], [a8]): The system (a5) is locally topologically equivalent near the origin to the suspension of (a7) by the standard saddle (a4). Moreover, (a7) can be replaced by any locally topologically equivalent system.
This theorem reduces the study of bifurcations of non-hyperbolic equilibria (cf. also Bifurcation) to those on the corresponding centre manifold of dimension equal to the number of critical eigenvalues. There are analogues of the reduction principle and Šošitaišvili's theorem for discrete-time dynamical systems defined by iterations of diffeomorphisms (see, for example, [a1], [a8]). Existence of centre manifolds has also been proved for certain infinite-dimensional dynamical systems defined by partial differential equations [a9], [a3], [a6] and delay differential equations [a5], [a4].
References
| [a1] | V.I. Arnol'd, "Geometrical methods in the theory of ordinary differential equations" , Grundlehren math. Wiss. , 250 , Springer (1983) (In Russian) |
| [a2] | V.I. Arnol'd, V.S. Afraimovich, Yu.S. Il'yashenko, L.P. Shil'nikov, "Bifurcation theory" V.I. Arnol'd (ed.) , Dynamical Systems V , Encycl. Math. Sci. , Springer (1994) (In Russian) |
| [a3] | J. Carr, "Applications of center manifold theory" , Springer (1981) |
| [a4] | O. Diekmann, S.A. van Gils, S.M. Verduyn Lunel, H.-O. Walther, "Delay equations" , Springer (1995) |
| [a5] | J. Hale, S.M. Verduyn Lunel, "Introduction to functional differential equations" , Springer (1993) |
| [a6] | D. Henry, "Geometric theory of semilinear parabolic equations" , Springer (1981) |
| [a7] | A. Kelley, "The stable, center stable, center, center unstable and unstable manifolds" J. Diff. Eq. , 3 (1967) pp. 546–570 |
| [a8] | Yu.A. Kuznetsov, "Elements of applied bifurcation theory" , Springer (1995) |
| [a9] | J. Marsden, M. McCracken, "Hopf bifurcation and its applications" , Springer (1976) |
| [a10] | A.N. Šošitaišvili, "Bifurcations of topological type of a vector field near a singular point" , Proc. Petrovskii Sem. , 1 , Moscow Univ. (1975) pp. 279–309 (In Russian) |
| [a11] | A. Vanderbauwhede, "Centre manifolds, normal forms and elementary bifurcations" Dynamics Reported , 2 (1989) pp. 89–169 |
Centre manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Centre_manifold&oldid=16865