Centre
A kind of pattern of the trajectories of an autonomous system of ordinary second-order differential equations (*) in a neighbourhood of a singular point 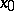 , where
, where
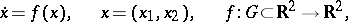 | (*) |
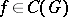 and
and 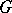 is a domain of uniqueness. This kind of pattern is characterized as follows. There exists a neighbourhood
is a domain of uniqueness. This kind of pattern is characterized as follows. There exists a neighbourhood 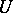 of
of 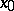 such that all trajectories of the system starting in
such that all trajectories of the system starting in 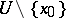 are closed curves going around
are closed curves going around 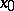 . Here the point
. Here the point 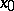 itself is also called a centre. In the figure the point 0 is the centre. The motion along trajectories with increasing
itself is also called a centre. In the figure the point 0 is the centre. The motion along trajectories with increasing 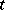 can proceed clockwise (indicated in the figure by arrows) or counterclockwise. A centre is Lyapunov stable (but not asymptotically stable). Its Poincaré index is 1.
can proceed clockwise (indicated in the figure by arrows) or counterclockwise. A centre is Lyapunov stable (but not asymptotically stable). Its Poincaré index is 1.

Figure: c021230a
A point 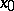 is a centre for a system (*), for example when
is a centre for a system (*), for example when 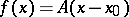 , where
, where 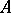 is a constant matrix with pure imaginary eigen values. In contrast to simple rest points of other types that occur for linear second-order systems (a saddle, a node or a focus), a point
is a constant matrix with pure imaginary eigen values. In contrast to simple rest points of other types that occur for linear second-order systems (a saddle, a node or a focus), a point 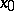 of centre-type does not, generally speaking, remain a centre under a perturbation of the right-hand side of the linear system, whatever the order of smallness of the perturbations relative to
of centre-type does not, generally speaking, remain a centre under a perturbation of the right-hand side of the linear system, whatever the order of smallness of the perturbations relative to  and the order of their smoothness may be. It can then change into a focus (stable or unstable) or into a centre-focus (see Centre and focus problem). For a non-linear system (*) of class
and the order of their smoothness may be. It can then change into a focus (stable or unstable) or into a centre-focus (see Centre and focus problem). For a non-linear system (*) of class  (
(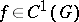 ) a rest point
) a rest point  can be a centre also in the case when the matrix
can be a centre also in the case when the matrix 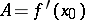 has two zero eigen values.
has two zero eigen values.
See also the references to Singular point of a differential equation.
References
| [1] | V.V. Amel'kin, N.A. Lukashevich, A.P. Sadovskii, "Non-linear oscillations in second-order systems" , Minsk (1982) (In Russian) |
Comments
For a precise topological definition see [a1], p. 71.
References
| [a1] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) |
| [a2] | A.A. Andronov, E.A. Leontovich, I.I. Gordon, A.G. Maier, "Theory of bifurcations of dynamic systems on a plane" , Israel Program Sci. Transl. (1971) (Translated from Russian) |
| [a3] | V.I. Arnol'd, "Geometrical methods in the theory of ordinary differential equations" , Springer (1983) (Translated from Russian) |
Centre. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Centre&oldid=13006