Central exponents
of a linear system of ordinary differential equations
Quantities defined by the formulas
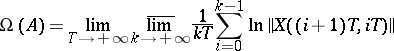 |
(the upper central exponent) and
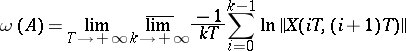 |
(the lower central exponent); sometimes the lower central exponent is defined as
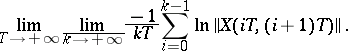 |
Here 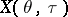 is the Cauchy operator of the system
is the Cauchy operator of the system
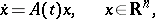 | (1) |
where 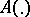 is a mapping
is a mapping
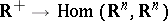 |
that is summable on every interval. The central exponents 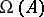 and
and 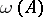 may be
may be 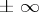 ; the inequalities
; the inequalities
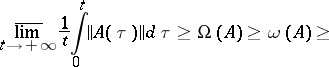 |
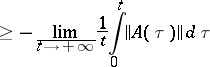 |
hold, which imply that if the system (1) satisfies the condition
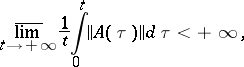 |
then its central exponents are finite numbers. The central exponents are connected with the Lyapunov characteristic exponents (cf. Lyapunov characteristic exponent) 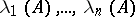 and with the singular exponents
and with the singular exponents 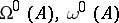 by the inequalities
by the inequalities
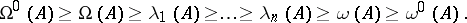 |
For a system (1) with constant coefficients 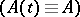 the central exponents
the central exponents 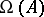 and
and 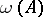 are equal, respectively, to the maximum and minimum of the real parts of the eigen values of
are equal, respectively, to the maximum and minimum of the real parts of the eigen values of 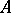 . For a system (1) with periodic coefficients (
. For a system (1) with periodic coefficients (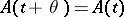 for all
for all 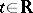 and some
and some 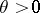 ,
, 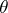 being the smallest period) the central exponents
being the smallest period) the central exponents 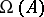 and
and 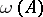 are equal, respectively, to the maximum and minimum of the logarithms of the moduli of the multipliers divided by the period
are equal, respectively, to the maximum and minimum of the logarithms of the moduli of the multipliers divided by the period 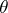 .
.
If 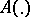 is an almost-periodic mapping (see Linear system of differential equations with almost-periodic coefficients), then the central exponents of (1) coincide with the singular exponents:
is an almost-periodic mapping (see Linear system of differential equations with almost-periodic coefficients), then the central exponents of (1) coincide with the singular exponents:
 |
(Bylov's theorem).
For every fixed system (1) the condition 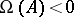 is sufficient for the existence of a
is sufficient for the existence of a 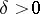 such that for every system
such that for every system
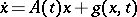 |
satisfying the conditions of the existence and uniqueness theorem for the solution of the Cauchy problem and the condition
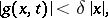 |
the solution 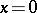 is asymptotically stable (Vinograd's theorem). The condition
is asymptotically stable (Vinograd's theorem). The condition 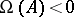 in Vinograd's theorem is not only sufficient but also necessary. (The necessity remains valid when asymptotic stability is replaced by Lyapunov stability.)
in Vinograd's theorem is not only sufficient but also necessary. (The necessity remains valid when asymptotic stability is replaced by Lyapunov stability.)
The function 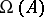 (respectively,
(respectively, 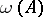 ) on the space
) on the space 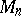 of the system (1) with bounded continuous coefficients (so that
of the system (1) with bounded continuous coefficients (so that 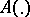 is continuous and
is continuous and  ), endowed with the metric
), endowed with the metric
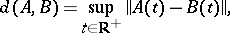 |
is upper (respectively lower) semi-continuous, but neither of these functions is continuous everywhere. For every system (1), in 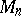 one can find another system
one can find another system
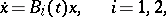 | (2) |
arbitrarily close to it (in 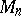 ) such that
) such that
 |
where 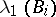 and
and 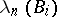 ,
, 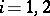 , are the largest (highest) and the smallest (least) characteristic Lyapunov exponents of the system (2).
, are the largest (highest) and the smallest (least) characteristic Lyapunov exponents of the system (2).
If  is a uniformly-continuous mapping and if
is a uniformly-continuous mapping and if 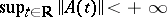 , then for almost-every mapping
, then for almost-every mapping 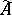 (in the sense of every normalized invariant measure of shift dynamical systems (cf. Shift dynamical system),
(in the sense of every normalized invariant measure of shift dynamical systems (cf. Shift dynamical system), 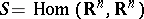 , concentrated on the closure of the trajectory of the point
, concentrated on the closure of the trajectory of the point 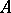 ; the mappings
; the mappings 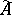 and
and 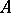 are regarded as points of the space of the shift dynamical system) the upper (lower) central exponent of the system
are regarded as points of the space of the shift dynamical system) the upper (lower) central exponent of the system 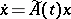 is equal to the largest (smallest) characteristic Lyapunov exponent of this system:
is equal to the largest (smallest) characteristic Lyapunov exponent of this system:
 |
Suppose that a dynamical system on a smooth closed manifold 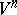 is given by a smooth vector field. Then for almost-every point
is given by a smooth vector field. Then for almost-every point 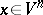 (in the sense of every normalized invariant measure) the upper (lower) central exponent of the system of equations in variations along the trajectory of
(in the sense of every normalized invariant measure) the upper (lower) central exponent of the system of equations in variations along the trajectory of  coincides with its largest (smallest) characteristic Lyapunov exponent. Generic properties of the central exponent (from the point of view of the Baire categories) have been studied, see .
coincides with its largest (smallest) characteristic Lyapunov exponent. Generic properties of the central exponent (from the point of view of the Baire categories) have been studied, see .
References
| [1] | B.F. Bylov, R.E. Vinograd, D.M. Grobman, V.V. Nemytskii, "The theory of Lyapunov exponents and its applications to problems of stability" , Moscow (1966) (In Russian) |
| [2] | N.A. Izobov, "Linear systems of ordinary differential equations" J. Soviet Math. , 5 : 1 (1974) pp. 46–96 Itogi Nauk. Mat. Anal , 12 pp. 71–146 |
| [3a] | V.M. Millionshchikov, "Typical properties of conditional exponential stability II" Differential equations , 19 : 9 pp. 1126–1132 Differentsial'nye Uravneniya , 19 : 9 (1983) pp. 1503–1510 |
| [3b] | V.M. Millionshchikov, "Typical properties of conditional exponential stability VI" Differential equations , 20 : 6 pp. 707–715 Differentsial'nye Uravneniya , 20 : 6 (1984) |
| [3c] | V.M. Millionshchikov, "Typical properties of conditional exponential stability VII" Differential equations , 20 : 8 pp. 1005–1013 Differentsial'nye Uravneniya , 20 : 8 (1984) pp. 1366–1376 |
Comments
References
| [a1] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) |
Central exponents. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Central_exponents&oldid=13711