Cell
A term sometimes used to denote a period parallelogram of a double-periodic function  whose sides do not contain poles, and which is obtained from a fundamental period parallelogram by translation over a vector
whose sides do not contain poles, and which is obtained from a fundamental period parallelogram by translation over a vector  .
.
References
| [1] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1927) |
Comments
In addition there are several technical meanings of the word cell in geometry and topology. Thus, in affine geometry the convex hull of a finite set of points is sometimes called a convex cell. A subset  of a topological Hausdorff space such that there is a relative homeomorphism
of a topological Hausdorff space such that there is a relative homeomorphism  is a (topological)
is a (topological)  -dimensional cell. Here
-dimensional cell. Here  is the unit ball, its boundary
is the unit ball, its boundary 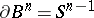 is the
is the  -dimensional sphere, and a relative homeomorphism is, of course, a continuous mapping
-dimensional sphere, and a relative homeomorphism is, of course, a continuous mapping 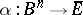 such that
such that 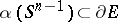 and
and  induces a homeomorphism
induces a homeomorphism 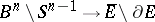 ; cf. also Cell complex and Cellular space. The phrase unit cell occasionally occurs as a synonym for the ball (disc) of radius one centred at the origin in
; cf. also Cell complex and Cellular space. The phrase unit cell occasionally occurs as a synonym for the ball (disc) of radius one centred at the origin in  -dimensional Euclidean space, and any space homeomorphic to it is also sometimes called an
-dimensional Euclidean space, and any space homeomorphic to it is also sometimes called an  -dimensional topological cell. Finally, cell is sometimes used to denote the possible locations of entries in a matrix or similar structure, such as a magic square or Young diagram, or as a synonym for a block in a block matrix.
-dimensional topological cell. Finally, cell is sometimes used to denote the possible locations of entries in a matrix or similar structure, such as a magic square or Young diagram, or as a synonym for a block in a block matrix.
Cell. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cell&oldid=15623