Cayley transform
of a linear (dissipative) operator  with domain
with domain  dense in a Hilbert space
dense in a Hilbert space 
The operator  , defined on the subspace
, defined on the subspace  . A matrix version of this transform was considered by A. Cayley. The Cayley transform establishes a correspondence between the properties of operators
. A matrix version of this transform was considered by A. Cayley. The Cayley transform establishes a correspondence between the properties of operators  with spectra
with spectra  "close" to the real line and operators with almost-unitary spectra (close to the circle
"close" to the real line and operators with almost-unitary spectra (close to the circle  ). The following propositions are true: 1) if
). The following propositions are true: 1) if  is a linear dissipative operator, then
is a linear dissipative operator, then 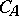 is a contraction (i.e.
is a contraction (i.e. 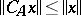 ,
, 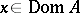 ) and
) and 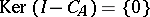 ; 2) if
; 2) if 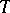 is a contraction,
is a contraction, 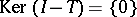 and
and 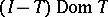 is dense in
is dense in 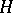 , then
, then 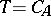 for some linear dissipative operator
for some linear dissipative operator  ; in fact,
; in fact, 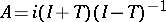 ; 3)
; 3) 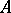 is symmetric (self-adjoint) if and only if
is symmetric (self-adjoint) if and only if 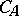 is isometric (unitary); 4)
is isometric (unitary); 4) 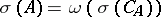 , where
, where 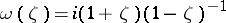 , in particular,
, in particular, 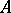 is bounded if and only if
is bounded if and only if 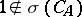 ; and 5) if
; and 5) if 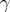 is an operator ideal in
is an operator ideal in 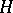 , then
, then  implies
implies 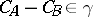 ; if
; if 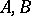 are bounded operators, then the converse is also valid:
are bounded operators, then the converse is also valid: 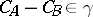 implies
implies 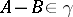 . The Cayley transform also establishes a correspondence between certain other characteristics of the operators
. The Cayley transform also establishes a correspondence between certain other characteristics of the operators 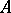 and
and 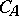 : classifications of parts of the spectrum, multiplicities of spectra, structures of invariant subspaces, functional calculi, spectral decompositions, etc. Thus, if
: classifications of parts of the spectrum, multiplicities of spectra, structures of invariant subspaces, functional calculi, spectral decompositions, etc. Thus, if 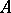 is a self-adjoint operator with resolution of the identity
is a self-adjoint operator with resolution of the identity  ,
, 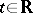 , then
, then 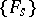 ,
, 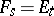 for
for 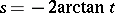 , is a resolution of the identity for
, is a resolution of the identity for 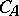 and
and
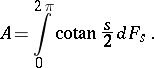 |
References
| [1] | N.I. Akhiezer, I.M. Glazman, "Theory of linear operators in Hilbert space" , 1–2 , Pitman (1981) (Translated from Russian) |
| [2] | B. Szökefalvi-Nagy, Ch. Foiaş, "Harmonic analysis of operators on Hilbert space" , North-Holland (1970) (Translated from French) |
Cayley transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cayley_transform&oldid=12556