Cayley form
A form in 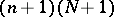 variables, where
variables, where 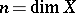 , with
, with 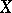 a closed algebraic subvariety of an
a closed algebraic subvariety of an 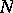 -dimensional projective space
-dimensional projective space 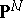 , which is determined by
, which is determined by 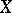 uniquely up to a constant factor and itself uniquely determines
uniquely up to a constant factor and itself uniquely determines 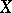 . The exact definition is as follows. Let
. The exact definition is as follows. Let 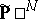 be the
be the 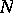 -dimensional projective space of all hyperplanes in
-dimensional projective space of all hyperplanes in 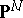 , and let
, and let 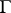 be the subset of the variety
be the subset of the variety
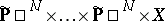 |
(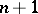 factors
factors  ) consisting of all
) consisting of all  -tuples
-tuples 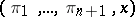 , where
, where 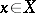 is a point in the intersection of the hyperplanes
is a point in the intersection of the hyperplanes 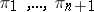 and
and
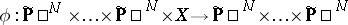 |
(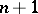 factors
factors  each time) is the natural projection. Then
each time) is the natural projection. Then 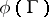 is an irreducible subvariety of codimension 1 in
is an irreducible subvariety of codimension 1 in
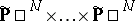 |
(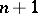 factors) and so
factors) and so 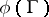 is the zero variety for some form
is the zero variety for some form 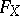 on
on
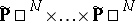 |
(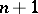 factors).
factors).
It may always be assumed that 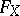 has no multiple factors, and this condition defines
has no multiple factors, and this condition defines 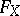 uniquely up to multiplication by a constant, given
uniquely up to multiplication by a constant, given 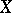 . Conversely,
. Conversely, 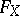 uniquely determines the set of all possible
uniquely determines the set of all possible 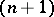 -tuples of hyperplanes in
-tuples of hyperplanes in 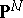 that intersect at points of
that intersect at points of  , and so
, and so 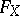 uniquely determines
uniquely determines  . The form
. The form 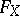 is called the Cayley form of
is called the Cayley form of 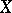 .
.
The Cayley form is also frequently known as the Chow form, or the associated form, of the variety  . The idea of defining
. The idea of defining 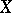 by the complex of linear subspaces of dimension
by the complex of linear subspaces of dimension 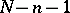 in
in  that intersect
that intersect 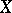 goes back to A. Cayley [5], who applied it to the case
goes back to A. Cayley [5], who applied it to the case 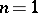 ,
, 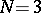 . The coefficients of the Cayley form are known as the Chow coordinates of the variety
. The coefficients of the Cayley form are known as the Chow coordinates of the variety  .
.
The Cayley form 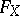 is homogeneous in each of the
is homogeneous in each of the 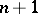 coordinate systems of the space
coordinate systems of the space
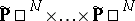 |
(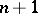 factors) (the
factors) (the 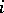 -th coordinate system is the coordinate system of the
-th coordinate system is the coordinate system of the 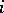 -th factor in this space). The form
-th factor in this space). The form 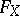 has the same degree of homogeneity with respect to each system; this common degree
has the same degree of homogeneity with respect to each system; this common degree 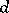 is denoted by
is denoted by 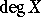 and is called the degree of the subvariety
and is called the degree of the subvariety  . It admits a geometrical interpretation:
. It admits a geometrical interpretation: 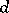 is the maximum number of points of intersection of
is the maximum number of points of intersection of  with all possible
with all possible 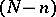 -dimensional linear spaces
-dimensional linear spaces 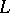 in
in 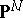 such that
such that 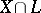 is a finite set (i.e.
is a finite set (i.e. 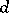 is the number of points in the intersection of
is the number of points in the intersection of  with a "general"
with a "general" 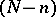 -dimensional linear subspace).
-dimensional linear subspace).
The set of all forms (up to multiplication by a non-zero constant) in 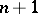 groups of variables consisting of
groups of variables consisting of 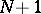 variables and having degree
variables and having degree 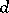 in each group, forms a projective space
in each group, forms a projective space  of dimension
of dimension 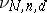 . The Cayley form
. The Cayley form 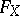 may be identified with a point of
may be identified with a point of  . The set
. The set  of all points in
of all points in 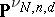 which are Cayley forms of
which are Cayley forms of  -dimensional closed subvarieties of degree
-dimensional closed subvarieties of degree 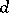 in
in 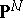 is a quasi-projective variety; it parametrizes the family of all such subvarieties in such a way that the family is algebraic relative to the parametrization. In general,
is a quasi-projective variety; it parametrizes the family of all such subvarieties in such a way that the family is algebraic relative to the parametrization. In general, 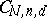 need not be closed in
need not be closed in 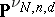 .
.
The construction of the Cayley form carries over in a natural way to closed  -dimensional cycles in
-dimensional cycles in 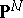 , i.e. to formal linear combinations
, i.e. to formal linear combinations 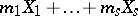 of closed
of closed  -dimensional subvarieties
-dimensional subvarieties 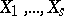 in
in 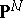 with integer coefficients
with integer coefficients  . In fact, one puts
. In fact, one puts
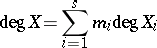 |
and  . The set
. The set 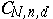 of all Cayley forms of
of all Cayley forms of  -dimensional cycles of degree
-dimensional cycles of degree 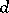 in
in 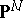 is closed in
is closed in 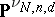 .
.
The investigation of Cayley forms and the properties of the varieties 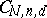 and
and 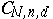 constitute an important aspect in the problem of classifying subvarieties and cycles in
constitute an important aspect in the problem of classifying subvarieties and cycles in  . The first stage in this classification is to study the decomposition of
. The first stage in this classification is to study the decomposition of 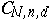 into irreducible components. For example, if
into irreducible components. For example, if 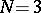 ,
, 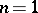 ,
, 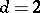 (curves of degree 2 in three-dimensional space), the variety
(curves of degree 2 in three-dimensional space), the variety 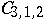 decomposes into two irreducible
decomposes into two irreducible 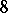 -dimensional components. The first corresponds to planar curves of the second order, the second to pairs of straight lines. The birational classification of the varieties
-dimensional components. The first corresponds to planar curves of the second order, the second to pairs of straight lines. The birational classification of the varieties 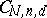 is an important problem (in all known examples these varieties are rational).
is an important problem (in all known examples these varieties are rational).
References
| [1] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
| [2] | W.V.D. Hodge, D. Pedoe, "Methods of algebraic geometry" , 2 , Cambridge Univ. Press (1952) |
| [3] | P. Samuel, "Méthodes d'algèbre abstraite en géométrie algébrique" , Springer (1955) |
| [4] | W.-L. Chow, B.L. van der Waerden, "Zur algebraische Geometrie IX" Math. Ann. , 113 (1937) pp. 692–704 |
| [5] | A. Cayley, "On a new analytical representation of curves in space" , Collected mathematical papers , 4 , Cambridge Univ. Press (1891) pp. 446–455 (Quart. J. Pure Appl. Math. 3 (1860), 225–236) |
Comments
The varieties 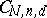 are special cases of Hilbert schemes (cf. Hilbert scheme).
are special cases of Hilbert schemes (cf. Hilbert scheme).
Cayley form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cayley_form&oldid=11497