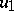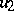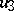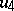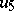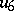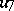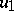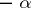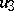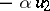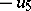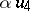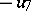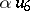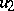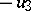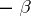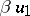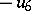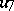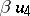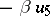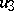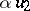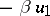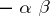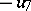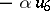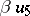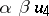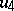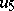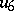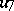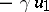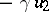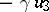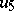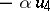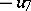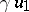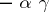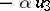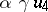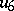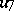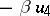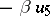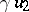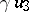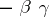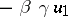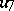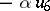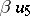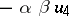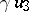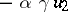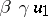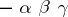Difference between revisions of "Cayley-Dickson algebra"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Cayley–Dickson algebra to Cayley-Dickson algebra: ascii title) |
(No difference)
| |
Revision as of 18:51, 24 March 2012
An alternative  -dimensional algebra, derived from the algebra of generalized quaternions via the Cayley–Dickson process (cf. Quaternion and Alternative rings and algebras). The latter starts out from a given algebra
-dimensional algebra, derived from the algebra of generalized quaternions via the Cayley–Dickson process (cf. Quaternion and Alternative rings and algebras). The latter starts out from a given algebra  to construct a new algebra
to construct a new algebra  (of twice the dimension of
(of twice the dimension of  ) and is a generalization of the doubling process (see Hypercomplex number). Namely, let
) and is a generalization of the doubling process (see Hypercomplex number). Namely, let  be an algebra with a unit 1 over a field
be an algebra with a unit 1 over a field  , let
, let  be some non-zero element of
be some non-zero element of  , and let
, and let  be an
be an 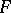 -linear mapping which is an involution, and such that
-linear mapping which is an involution, and such that
 |
The formula
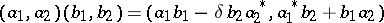 |
now defines a multiplication operation on the direct sum of linear spaces 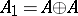 , relative to which
, relative to which 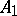 is an algebra. The algebra
is an algebra. The algebra 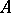 may be imbedded in
may be imbedded in  as a subalgebra:
as a subalgebra: 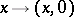 , and the involution
, and the involution  extends to an involution in
extends to an involution in 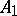 :
:
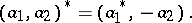 |
Moreover,
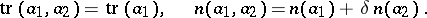 |
The extension of 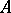 to
to 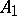 can be repeated resulting in an ascending chain of algebras
can be repeated resulting in an ascending chain of algebras 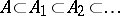 ; the parameter
; the parameter 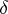 need not be the same at each stage. If the Cayley–Dickson process is begun with an algebra
need not be the same at each stage. If the Cayley–Dickson process is begun with an algebra  with basis
with basis  , multiplication table
, multiplication table
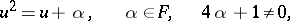 |
and involution 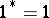 ,
, 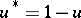 , the first application of the process yields an algebra
, the first application of the process yields an algebra 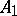 of generalized quaternions (an associative algebra of dimension 4), and the second — an
of generalized quaternions (an associative algebra of dimension 4), and the second — an 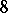 -dimensional algebra, known as a Cayley–Dickson algebra.
-dimensional algebra, known as a Cayley–Dickson algebra.
Any Cayley–Dickson algebra is an alternative, but non-associative, central simple algebra over 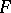 ; conversely, a simple alternative ring is either associative or a Cayley–Dickson algebra over its centre. The quadratic form
; conversely, a simple alternative ring is either associative or a Cayley–Dickson algebra over its centre. The quadratic form 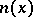 in 8 variables defined on a Cayley–Dickson algebra (the 8 variables correspond to the basis elements) has the multiplicative property:
in 8 variables defined on a Cayley–Dickson algebra (the 8 variables correspond to the basis elements) has the multiplicative property:
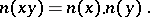 |
This establishes a connection between Cayley–Dickson algebras and the existence problem for compositions of quadratic forms. A Cayley–Dickson algebra is a division algebra if and only if the quadratic form 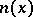 (the norm of
(the norm of  ) does not represent the zero in
) does not represent the zero in 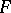 . If
. If 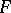 is a field of characteristic other than 2, a Cayley–Dickson algebra has a basis
is a field of characteristic other than 2, a Cayley–Dickson algebra has a basis 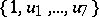 with the following multiplication table:'
with the following multiplication table:'
<tbody> </tbody>
|
where 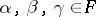 ,
,  , and the involution is defined by the conditions
, and the involution is defined by the conditions
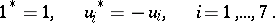 |
This algebra is denoted by 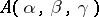 . The algebras
. The algebras 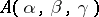 and
and 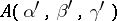 are isomorphic if and only if their quadratic forms
are isomorphic if and only if their quadratic forms 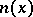 are equivalent. If
are equivalent. If 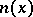 represents zero, the corresponding Cayley–Dickson algebra is isomorphic to
represents zero, the corresponding Cayley–Dickson algebra is isomorphic to  , which is known as the Cayley splitting algebra, or the vector-matrix algebra. Its elements may be expressed as matrices
, which is known as the Cayley splitting algebra, or the vector-matrix algebra. Its elements may be expressed as matrices
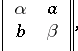 |
where 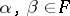 ,
, 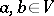 , with
, with 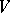 a three-dimensional space over
a three-dimensional space over  with the usual definition of the scalar product
with the usual definition of the scalar product 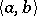 and vector product
and vector product 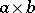 . Matrix multiplication is defined by
. Matrix multiplication is defined by
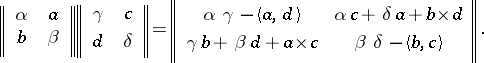 |
If 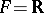 is the real field, then
is the real field, then 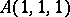 is the algebra of Cayley numbers (a division algebra). Any Cayley–Dickson algebra over
is the algebra of Cayley numbers (a division algebra). Any Cayley–Dickson algebra over 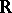 is isomorphic to either
is isomorphic to either 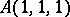 or
or 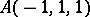 .
.
The construction of Cayley–Dickson algebras over an arbitrary field is due to L.E. Dickson, who also investigated their fundamental properties (see [1], [2]).
Let 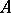 be an alternative ring whose associative-commutative centre
be an alternative ring whose associative-commutative centre 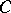 is distinct from zero and does not contain zero divisors; let
is distinct from zero and does not contain zero divisors; let  be the field of fractions of
be the field of fractions of 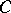 . Then there is a natural imbedding
. Then there is a natural imbedding 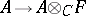 . If
. If  is a Cayley–Dickson algebra over
is a Cayley–Dickson algebra over  , then
, then 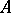 is known as a Cayley–Dickson ring.
is known as a Cayley–Dickson ring.
References
| [1] | L.E. Dickson, "Linear algebras" , Cambridge Univ. Press (1930) |
| [2] | R.D. Schafer, "An introduction to nonassociative algebras" , Acad. Press (1966) |
| [3] | K.A. Zhevlakov, A.M. Slin'ko, I.P. Shestakov, A.I. Shirshov, "Rings that are nearly associative" , Acad. Press (1982) (Translated from Russian) |
Cayley-Dickson algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cayley-Dickson_algebra&oldid=22269