Cauchy theorem
Cauchy's theorem on polyhedra: Two closed convex polyhedra are congruent if their true faces, edges and vertices can be put in an incidence-preserving one-to-one correspondence in such a way that corresponding faces are congruent. This is the first theorem about the unique definition of convex surfaces, since the polyhedra of which it speaks are isometric in the sense of an intrinsic metric. The Cauchy theorem is a special case of the theorem stating that every closed convex surface is uniquely defined by its metric (see [4]).
The theorem was first proved by A.L. Cauchy (see [1]).
References
| [1] | A.L. Cauchy, J. Ecole Polytechnique , 9 (1813) pp. 87–98 |
| [2] | A.D. Aleksandrov, "Konvexe Polyeder" , Akademie Verlag (1958) (Translated from Russian) |
| [3] | J. Hadamard, "Géométrie élémentaire" , 2 , Moscow (1957) (In Russian; translated from French) |
| [4] | A.V. Pogorelov, "Unique definition of convex surfaces" Trudy Mat. Inst. Steklov. , 29 (1949) (In Russian) |
E.V. Shikin
Cauchy's intermediate-value theorem for continuous functions on closed intervals: Let 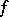 be a continuous real-valued function on
be a continuous real-valued function on 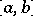 and let
and let 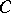 be a number between
be a number between 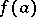 and
and 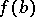 . Then there is a point
. Then there is a point 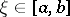 such that
such that 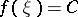 . In particular, if
. In particular, if 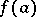 and
and 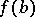 have different signs, then there is a point
have different signs, then there is a point 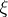 such that
such that 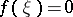 . This version of Cauchy's theorem is used to determine intervals in which a function necessarily has zeros. It follows from Cauchy's theorem that the image of an interval on the real line under a continuous mapping into the real line is also an interval. The theorem can be generalized to topological spaces: Any continuous function
. This version of Cauchy's theorem is used to determine intervals in which a function necessarily has zeros. It follows from Cauchy's theorem that the image of an interval on the real line under a continuous mapping into the real line is also an interval. The theorem can be generalized to topological spaces: Any continuous function  defined on a connected topological space
defined on a connected topological space 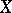 and assuming two distinct values, also assumes any value between them; hence the image of
and assuming two distinct values, also assumes any value between them; hence the image of 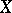 is also an interval on the real line.
is also an interval on the real line.
Cauchy's theorem was formulated independently by B. Bolzano (1817) and by A.L. Cauchy (1821).
Cauchy's intermediate-value theorem is a generalization of Lagrange's mean-value theorem. If 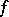 and
and 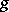 are continuous real functions on
are continuous real functions on 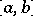 and differentiable in
and differentiable in 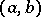 , with
, with 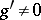 on
on 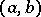 (and therefore
(and therefore 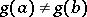 ), then there exists a point
), then there exists a point 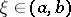 such that
such that
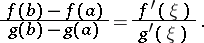 |
Putting 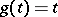 ,
, 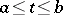 , one obtains the ordinary Lagrange mean-value theorem. In geometrical terms, Cauchy's theorem means that on any continuous curve
, one obtains the ordinary Lagrange mean-value theorem. In geometrical terms, Cauchy's theorem means that on any continuous curve 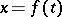 ,
, 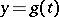 ,
, 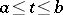 , in the
, in the 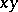 -plane having a tangent at each point
-plane having a tangent at each point 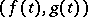 , there exists a point
, there exists a point 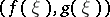 at which the tangent is parallel to the chord connecting the end points
at which the tangent is parallel to the chord connecting the end points 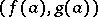 and
and 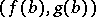 of the curve.
of the curve.
References
| [1] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian) |
| [2] | L.D. Kudryavtsev, "Mathematical analysis" , 1 , Moscow (1973) (In Russian) |
| [3] | S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) (Translated from Russian) |
L.D. Kudryavtsev
Comments
The statement in
can be generalized. For continuous real functions 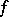 and
and  on
on 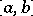 that are differentiable in
that are differentiable in 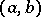 there is an
there is an 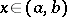 at which
at which
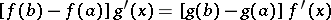 |
(cf. [a1]).
References
| [a1] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1976) pp. 107–108 |
Cauchy's theorem in group theory: If the order of a finite group 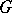 is divisible by a prime number
is divisible by a prime number 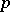 , then
, then 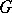 contains an element of order
contains an element of order 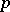 .
.
This theorem was first proved by A.L. Cauchy (see [1]) for permutation groups.
References
| [1] | A.L. Cauchy, "Exercise d'analyse et de physique mathématique" , 3 , Paris (1844) pp. 151–252 |
| [2] | A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian) |
Comments
References
| [a1] | M. Suzuki, "Group theory" , 1 , Springer (1982) |
Cauchy theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cauchy_theorem&oldid=16651