Cauchy kernel

The function of the form , which is the kernel of the Cauchy integral. In the case of the unit circle one has the following relationship between the Cauchy kernel and the Hilbert kernel:

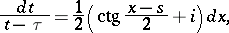where

The term Cauchy kernel is sometimes applied to the function

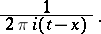Comments

See also Kernel function; Kernel of an integral operator.

References

[a1]	A.I. Markushevich, "Theory of functions of a complex variable" , 1–3 , Chelsea (1977) (Translated from Russian)
[a2]	E.C. Titchmarsh, "Introduction to the theory of Fourier integrals" , Oxford Univ. Press (1948)
[a3]	W. Rudin, "Real and complex analysis" , McGraw-Hill (1974) pp. 24