Cauchy integral theorem
If 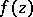 is a regular analytic function of a complex variable
is a regular analytic function of a complex variable  in a simply-connected domain
in a simply-connected domain 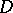 in the complex plane
in the complex plane 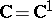 , then the integral of
, then the integral of 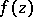 along any closed rectifiable curve
along any closed rectifiable curve 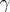 in
in 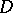 vanishes:
vanishes:
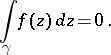 |
An equivalent version of Cauchy's integral theorem states that the integral
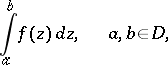 |
is independent of the choice of the path of integration between the fixed points  and
and 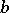 in
in 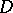 . This, essentially, was the original formulation of the theorem as proposed by A.L. Cauchy (1825) (see [1]); similar formulations may be found in the letters of C.F. Gauss (1811). Cauchy's proof involved the additional assumption that the derivative
. This, essentially, was the original formulation of the theorem as proposed by A.L. Cauchy (1825) (see [1]); similar formulations may be found in the letters of C.F. Gauss (1811). Cauchy's proof involved the additional assumption that the derivative 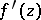 is continuous; the first complete proof was given by E. Goursat [2]. The property of analytic functions expressed by the Cauchy integral theorem fully characterizes them (see Morera theorem), and therefore all the fundamental properties of analytic functions may be inferred from the Cauchy integral theorem.
is continuous; the first complete proof was given by E. Goursat [2]. The property of analytic functions expressed by the Cauchy integral theorem fully characterizes them (see Morera theorem), and therefore all the fundamental properties of analytic functions may be inferred from the Cauchy integral theorem.
For an arbitrary domain 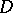 in the plane
in the plane 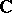 or on a Riemann surface, the Cauchy integral theorem may be stated as follows: If
or on a Riemann surface, the Cauchy integral theorem may be stated as follows: If 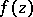 is a regular analytic function in the domain
is a regular analytic function in the domain 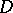 , then the integral of
, then the integral of 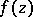 along any rectifiable closed curve
along any rectifiable closed curve 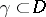 which is homotopic to zero in
which is homotopic to zero in 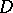 vanishes.
vanishes.
A generalization of the Cauchy integral theorem to analytic functions of several complex variables is the Cauchy–Poincaré theorem: If 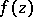 ,
, 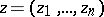 , is a regular analytic function in a domain
, is a regular analytic function in a domain 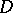 of the complex space
of the complex space 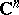 ,
, 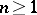 , then, for any
, then, for any 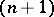 -dimensional surface
-dimensional surface 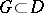 with smooth boundary
with smooth boundary 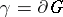 ,
,
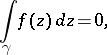 |
where 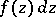 is an abbreviation for the holomorphic differential form
is an abbreviation for the holomorphic differential form
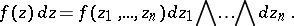 |
When 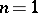 the surface
the surface 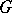 and the domain
and the domain 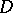 have the same dimension,
have the same dimension, 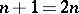 (the case of the classical Cauchy integral theorem); when
(the case of the classical Cauchy integral theorem); when 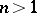 ,
, 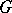 has lower dimension than
has lower dimension than 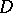 ,
, 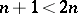 . See also Residue of an analytic function; Cauchy integral.
. See also Residue of an analytic function; Cauchy integral.
References
| [1] | A.L. Cauchy, "Oeuvres complètes, Ser. 1" , 4 , Paris (1890) |
| [2] | E. Goursat, "Démonstration du théorème de Cauchy" Acta Math. , 4 (1884) pp. 197–200 |
| [3] | A.I. Markushevich, "Theory of functions of a complex variable" , 1–2 , Chelsea (1977) (Translated from Russian) |
| [4] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
| [5] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) |
Comments
In [2] Goursat still assumed continuity of 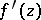 . He soon saw how to remove this assumption, cf. [a1].
. He soon saw how to remove this assumption, cf. [a1].
References
| [a1] | E. Goursat, "Sur la définition générale des fonctions analytiques, d'après Cauchy" Trans. Amer. Math. Soc. , 1 (1900) pp. 14–16 |
Cauchy integral theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cauchy_integral_theorem&oldid=31225