Cauchy integral

A Cauchy integral is a definite integral of a continuous function of one real variable. Let 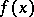be a continuous function on an interval 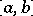and let 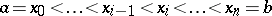, , 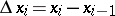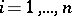. The limit

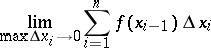is called the definite integral in Cauchy's sense of over and is denoted by

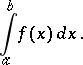The Cauchy integral is a particular case of the Riemann integral. The definition is due to A.L. Cauchy [1].

References

[1]	A.L. Cauchy, "Résumé des leçons données à l'Ecole Royale Polytechnique sur le calcul infinitésimal" , 1 , Paris (1823)

A Cauchy integral is an integral with the Cauchy kernel,

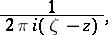expressing the values of a regular analytic function in the interior of a contour 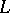in terms of its values on 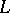. More precisely: Let 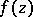be a regular analytic function of the complex variable in a domain 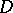and let 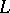be a closed piecewise-smooth Jordan curve lying in together with its interior 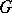; it is assumed that is described in the counter-clockwise sense. Then one has the following formula, which is of fundamental importance in the theory of analytic functions of one complex variable and which is known as the Cauchy integral formula:

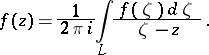(1)

The integral on the right of (1) is also called a Cauchy integral.

Apparently, the Cauchy integral first appeared, in certain special cases, in the work of A.L. Cauchy [1].

Cauchy integrals are thus characterized by two conditions: 1) they are evaluated along a closed, smooth (or, at least, piecewise-smooth) curve 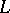; and 2) their integrands have the form

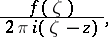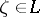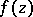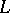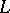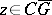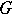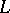where and is a regular analytic function on and in the interior of . If (the complement to ) in the Cauchy integral, i.e. if lies outside , then, provided that the conditions 1) and 2) remain valid,

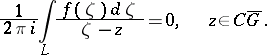(2)

In particular, if 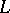is the circle of radius 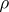centred at a point , i.e.

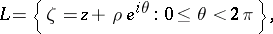then (1) implies that

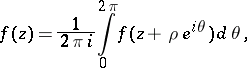i.e. the value of 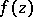at any point 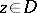is equal to the arithmetic average of its values on any sufficiently small circle 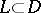centred at . Formula (1) enables one to prove all other elementary properties of analytic functions.

On the other hand, if 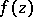is a regular analytic function in the infinite domain 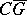(the exterior of the closed curve 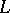) and on , and if one defines

then the following formula, known as the Cauchy integral formula for an infinite domain, is valid:

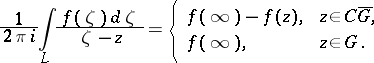Now let be some (not necessarily closed) piecewise-smooth curve in the finite plane, 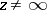, let be a continuous complex function on 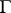and let be a point not on 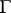. The term integral of Cauchy type is applied to the following generalization of the Cauchy integral:

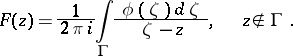(3)

The function 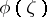is called the density of the integral of Cauchy type. Elementary properties of integrals of Cauchy type are:

1) 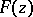is a regular analytic function of in any domain not containing points of .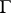

2) The derivatives 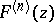are given by the formulas

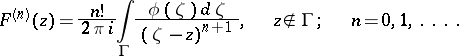3) 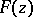is regular at infinity, with 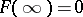, 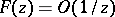as .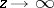

From the point of view of the general theory of analytic functions and its applications to mechanics and physics, it is of fundamental importance to consider the existence of boundary values of an integral of Cauchy type as one approaches 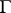, and to find analytic expressions for these values. The Cauchy integral (1) is equal to everywhere in the interior of 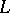and vanishes identically outside 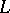. Therefore, when an integral of Cauchy type (3) reduces to a Cauchy integral, i.e. when the conditions 1) and 2) are satisfied, then, as 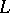is approached from the left (i.e. 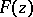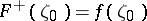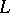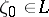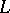from its interior), the function has boundary values , and if these values are assumed on it is continuous from the left on at each point ; as is approached from the right (i.e. from its exterior), then has boundary values zero, i.e. 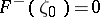, and if these values are assumed on 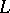it is continuous from the right on at each point 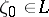. Thus, for a Cauchy integral

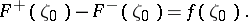For an integral of Cauchy type of general form the matter is somewhat more complicated. Suppose that the equation of the curve 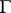is , where denotes the arc length reckoned from some fixed point, let 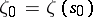be an arbitrary fixed point on 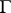and let 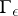be the part of 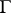that remains after the smaller of the arcs with end points 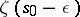and 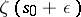is deleted from 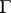. If the limit

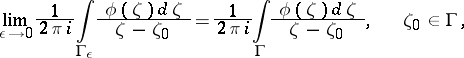(4)

exists and is finite, it is called a singular integral. It can be proved, for example, that a singular integral (4) exists if the curve 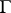is smooth in a neighbourhood of a point distinct from the end points of 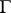and if the density satisfies a Hölder condition

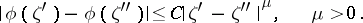Under these conditions there also exist boundary values, and these are given by the Sokhotskii formulas:

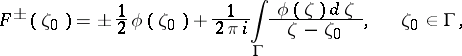(5)

and the functions 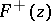and 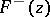are continuous in a neighbourhood of from the left and right, respectively, of 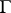. In the case of a Cauchy integral, the singular integral is equal to

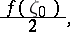An equivalent form of (5) is

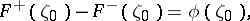(6)

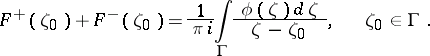(7)

The Sokhotskii formulas (5)–(7) are of fundamental importance in the solution of boundary value problems of analytic function theory, of singular integral equations connected with integrals of Cauchy type (cf. Singular integral equation), and also in the solution of various problems in hydrodynamics, elasticity theory, etc.

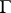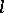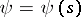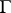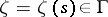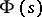Let be an arbitrary rectifiable curve of length ; for simplicity it is assumed that is closed. Let be the angle between the direction of the -axis and the tangent to at the point , regarded as a function of the arc length , and let be a complex function of of bounded variation on 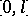. The expression

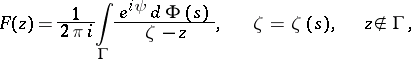(8)

is called an integral of Cauchy–Stieltjes type. In other words, an integral of Cauchy–Stieltjes type is an integral of Cauchy type with respect to an arbitrary finite complex Borel measure with support on 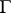. If 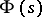is absolutely continuous, then the integral of Cauchy–Stieltjes type becomes an integral of Cauchy–Lebesgue type, often called simply an integral of Cauchy type:

(9)

where .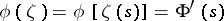

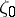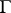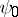Let be a point of at which there exists a well-defined tangent, inclined to the -axis at an angle ; such points exist almost-everywhere on a rectifiable curve. Let be the point on the straight line passing through 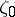and inclined to the normal at an angle 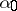, at a distance , i.e. . The difference between the integral of Cauchy–Stieltjes type (8) and the integral over ,

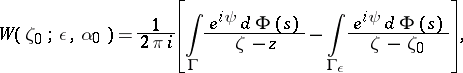is defined at all points 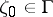where the tangent is defined, i.e. almost-everywhere on 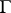. An important proposition in the theory of integrals of Cauchy–Stieltjes type is Privalov's fundamental lemma: The limit

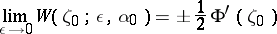exists for all points 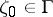, with the possible exception of a point set of measure zero on , independent of ; the convergence is uniform in in any angle 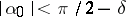, 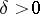. If the singular integral exists almost-everywhere on 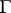, then the integral of Cauchy–Stieltjes type has angular boundary values almost-everywhere on and these satisfy the Sokhotskii formulas:

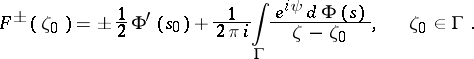(10)

The converse is also true: If an integral of Cauchy–Stieltjes type has angular boundary values from both inside and outside 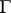, almost-everywhere on 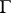, then the singular integral exists and formulas (10) are valid almost-everywhere on . As yet (1987) there is no complete solution to the problem of finding reasonably simple necessary and sufficient conditions for the existence of boundary values for integrals of Cauchy–Stieltjes type or even for integrals of Cauchy–Lebesgue type.

In contrast to the previously considered case of an integral of Cauchy type over a smooth curve 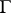, an integral of Cauchy–Stieltjes type, even when it has angular boundary values, is no longer necessarily a continuous function in a neighbourhood of 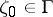from the left or right of 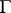. It is known, for example, that an integral of Cauchy–Lebesgue type (9) is continuous in the closed domain bounded by the rectifiable contour 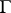, provided one additionally assumes that the density 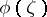satisfies a Lipschitz condition on :

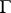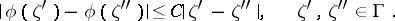One says that an integral of Cauchy–Lebesgue type (9) becomes a Cauchy integral

(11)

in the sense of Lebesgue, if the angular boundary values 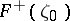from the inside of 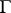coincide with 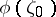almost-everywhere on 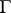, i.e. 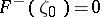almost-everywhere on 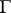. In this context the Golubev–Privalov theorem holds: A summable function on 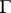represents the angular boundary values of some Cauchy integral from the inside of 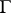if and only if all its moments vanish:

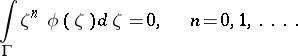(12)

If the analogous conditions

(13)

are satisfied, then the integral of Cauchy–Stieltjes type (8) becomes a Cauchy–Stieltjes integral:

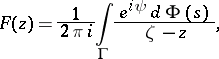(14)

i.e. the angular boundary values 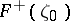from the inside of 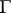coincide with the derivative 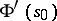almost-everywhere on , or, stated differently, the angular boundary values 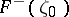from the outside of 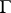vanish almost-everywhere on 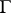. Conditions (13) immediately imply that the function is absolutely continuous on 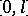and, consequently, in this case the Cauchy–Stieltjes integral (14) is in fact a Cauchy–Lebesgue integral with density 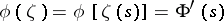. Thus, the class of functions representable by a Cauchy–Stieltjes integral is identical with the class of functions representable by a Cauchy–Lebesgue integral.

An important problem is the intrinsic characterization of classes of functions which are regular in a domain 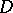bounded by a closed rectifiable curve 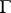, and representable by a Cauchy integral (11), an integral of Cauchy–Lebesgue type (9), or an integral of Cauchy–Stieltjes type (8); concerning the most important classes 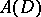, , 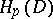and 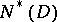see Boundary properties of analytic functions.

In the simplest case, when 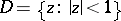is the unit disc and 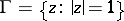is the unit circle, an integral of Cauchy–Stieltjes type, which in this case has the form

(15)

always represents a function of class , . The converse is false: The set of functions of classes , , 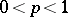is more extensive than the set of functions representable in the form (15). On the other hand, the set of functions representable in 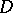by a Cauchy–Stieltjes or a Cauchy integral is identical with the class .

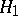In the case of an arbitrary simply-connected domain 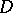bounded by a rectifiable curve 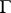, the class of functions representable in 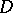by a Cauchy–Stieltjes or a Cauchy integral is identical with the Smirnov class 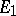(see Boundary properties of analytic functions). The characteristics of the classes of functions representable by an integral of Cauchy–Stieltjes type or an integral of Cauchy–Lebesgue type are considerably more complicated.

Let 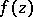be an arbitrary (non-analytic) function of class 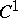in a finite closed domain 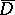bounded by a piecewise-smooth Jordan curve 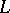. The term Cauchy integral formula is sometimes applied also to the following generalization of the classical formula (1):

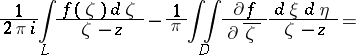(16)

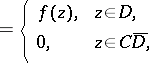where

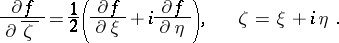This formula first appeared, apparently, in the work of D. Pompeiu (1912). It is also known as the Pompeiu formula, the Borel–Pompeiu formula, or the Cauchy–Green formula, and is widely applied in the theory of generalized analytic functions, singular integral equations and various applied problems.

Let 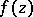be a regular analytic function of several complex variables 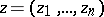in a closed polydisc 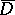, 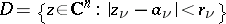. Then, at each point of 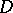, 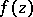is representable by a multiple Cauchy integral:

(17)

where 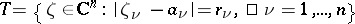is the distinguished boundary of the polydisc, 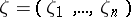, , 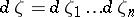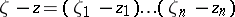. Formula (17) yields a simple analogue of the Cauchy integral for a circle 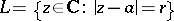, but when 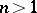the integration in (17) extends not over the entire boundary of the polydisc but only over its distinguished boundary. In general, let 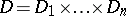be a polycircular domain in 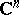— a product of simply-connected plane domains 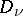with smooth boundaries 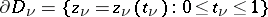; let be the distinguished boundary of 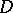, which is a smooth -dimensional manifold. Formula (17) also generalizes to this case.

More profound generalizations of the Cauchy integral formula are extremely important in the theory of analytic functions of several complex variables; such generalizations are the Leray formula (which J. Leray himself called the Cauchy–Fantappié formula) and the Bochner–Martinelli representation formula. In this connection, when 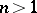the theory is concerned mainly with boundary properties of integral representations other than (17).

References

[1]	A.L. Cauchy, "Sur la mécanique céleste et sur un nouveau calcul appelé calcul des limites" , Turin (1831)
[2]	B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian)
[3]	A.I. Markushevich, "Theory of functions of a complex variable" , 1–3 , Chelsea (1977) (Translated from Russian)
[4]	N.I. Muskhelishvili, "Singular integral equations" , Wolters-Noordhoff (1972) (Translated from Russian)
[5]	V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian)
[6]	I.I. Privalov, "The Cauchy integral" , Saratov (1918) (In Russian)
[7]	I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)
[8]	S.Ya. Khavinson, Itogi Nauk. Mat. Anal. 1963 (1965) pp. 5–80
[9]	B.V. Khvedelidze, "The method of Cauchy type integrals in discontinuous boundary value problems of the theory of holomorphic functions of a complex variable" , Contemporary problems in mathematics , 7 , Moscow (1975) pp. 5–162 (In Russian)
[10]	A.P. Calderón, "Cauchy integrals on Lipschitz curves and related operators" Proc. Nat. Acad. Sci. USA , 74 : 4 (1977) pp. 1324–1327

Comments

In the non-Soviet literature Plemelj formulas is the usual name for what is here called Sokhotskii formulas.

Mapping properties of the singular integral operator associated to integrals of Cauchy type form an important subject. Let 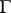be the graph of a Lipschitz function . The principal result, due to A.P. Calderón and in full generality to G. David, is that the singular integral operator

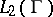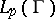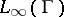at first defined as a principal value integral for compactly supported smooth functions on , extends to a bounded linear operator sending to itself, and (hence) also sending to itself and to 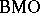, the functions of bounded mean oscillation.

Formally one can write:

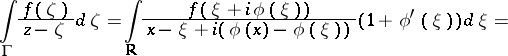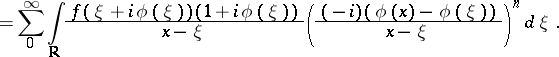The integral operators 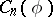with kernel

are the so-called commutators of Calderón. These are of independent interest, e.g. in the theory of partial differential equations (cf. Differential equation, partial). The operators 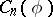have the same mapping properties as the Cauchy integral operator, as was shown by R.R. Coifman, A. McIntosh and Y. Meyer. The best norm estimate known at this moment (1987) is that for every 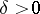there exists a 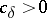such that

This estimate was obtained by M. Christ and J.L. Journé.

The Cauchy integral operators as well as Calderón's commutators are examples of so-called Calderón–Zygmund operators. For these results and further references see [10], [a2], [a3], [a4].

For results concerning 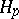functions, 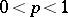, which can be represented by Cauchy integrals, see [a1].

References

[a1]	A.B. Aleksandrov, "Essays on non locally convex Hardy classes" V.P. Havin [V.P. Khavin] (ed.) N.K. Nikol'skii (ed.) , Complex analysis and spectral theory , Springer (1981) pp. 1–89
[a2]	M. Christ, J.L. Journé, "Estimates for multilinear singular integral operators with polynomial growth" (1986) (Preprint Dept. of Math. Princeton Univ.)
[a3]	R.R. Coifman, Y. Meyer, "Non linear harmonic analysis, operator theory and P.D.E." E.M. Stein (ed.) , Beijing lectures in harmonic analysis , Princeton Univ. Press (1986) pp. 3–46
[a4]	J.L. Journé, "Calderón–Zygmund operators, pseudodifferential operators and the Cauchy integral of Calderón" , Springer (1983)