Cauchy distribution
A continuous probability distribution with density
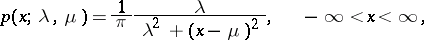 |
and distribution function
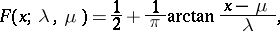 |
where 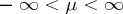 and
and 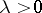 are parameters. The Cauchy distribution is unimodal and symmetric about the point
are parameters. The Cauchy distribution is unimodal and symmetric about the point 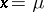 , which is its mode and median. No moments of positive order — including the expectation — exist. The characteristic function has the form
, which is its mode and median. No moments of positive order — including the expectation — exist. The characteristic function has the form 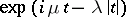 . The class of Cauchy distributions is closed under linear transformations: If a random variable
. The class of Cauchy distributions is closed under linear transformations: If a random variable  has the Cauchy distribution with parameters
has the Cauchy distribution with parameters  and
and 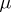 , then the random variable
, then the random variable 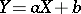 also has a Cauchy distribution, with parameters
also has a Cauchy distribution, with parameters 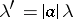 and
and 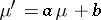 . The class of Cauchy distributions is closed under convolution:
. The class of Cauchy distributions is closed under convolution:
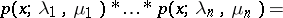 | (*) |
 |
in other words, a sum of independent random variables with Cauchy distributions is again a random variable with a Cauchy distribution. Thus, the Cauchy distribution, like the normal distribution, belongs to the class of stable distributions; to be precise: It is a symmetric stable distribution with index 1 (cf. Stable distribution). The following property of Cauchy distributions is a corollary of (*): If 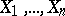 are independent random variables with the same Cauchy distribution, then their arithmetic mean
are independent random variables with the same Cauchy distribution, then their arithmetic mean 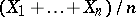 has the same distribution as each
has the same distribution as each 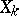 . One more property of Cauchy distributions: In the family of Cauchy distributions, the distribution of a sum of random variables may be given by (*) even if the variables are dependent. For example, if
. One more property of Cauchy distributions: In the family of Cauchy distributions, the distribution of a sum of random variables may be given by (*) even if the variables are dependent. For example, if 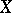 and
and 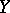 are independent and have the same Cauchy distribution, then the random variables
are independent and have the same Cauchy distribution, then the random variables 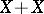 and
and  have the same Cauchy distribution. The Cauchy distribution with parameters
have the same Cauchy distribution. The Cauchy distribution with parameters 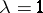 and
and  is the Student
is the Student 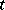 -distribution with one degree of freedom. The Cauchy distribution with parameters
-distribution with one degree of freedom. The Cauchy distribution with parameters 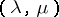 is identical with the distribution of the random variable
is identical with the distribution of the random variable 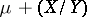 , where
, where 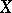 and
and 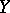 are independent and normally distributed with parameters
are independent and normally distributed with parameters 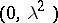 and
and  , respectively. A random variable with this distribution is the function
, respectively. A random variable with this distribution is the function 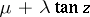 , where
, where  is a random variable uniformly distributed on the interval
is a random variable uniformly distributed on the interval 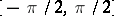 . The Cauchy distribution is also defined in spaces of dimension greater than one. The concept was first investigated by A.L. Cauchy.
. The Cauchy distribution is also defined in spaces of dimension greater than one. The concept was first investigated by A.L. Cauchy.
References
| [1] | W. Feller, "An introduction to probability theory and its applications" , 2 , Wiley (1966) |
Cauchy distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cauchy_distribution&oldid=11596