Cauchy characteristic problem
The problem of finding a solution of a partial differential equation (or a system of partial differential equations) which assumes prescribed values on a characteristic manifold.
There is a large class of equations of hyperbolic and parabolic types for which a non-closed  -dimensional surface
-dimensional surface  , oriented in a certain way, may serve as the initial surface in the space
, oriented in a certain way, may serve as the initial surface in the space 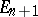 of independent variables
of independent variables 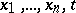 . For example, if
. For example, if  is a space-like surface then the Cauchy problem (with initial data on
is a space-like surface then the Cauchy problem (with initial data on  ) is always well-posed. In a characteristic Cauchy problem the initial surface is always a characteristic manifold (or a well-defined part thereof). In this case the Cauchy problem may have no solution at all; and if it has a solution it need not be unique.
) is always well-posed. In a characteristic Cauchy problem the initial surface is always a characteristic manifold (or a well-defined part thereof). In this case the Cauchy problem may have no solution at all; and if it has a solution it need not be unique.
For example, the characteristic Cauchy problem for the equation (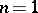 ,
, 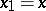 )
)
 |
with data on the characteristic  :
:
 |
is not well-posed. If the characteristic Cauchy problem has a solution, then the equation and the second initial condition imply a necessary condition for its solvability: 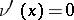 , i.e. the characteristic Cauchy problem may be solvable only if
, i.e. the characteristic Cauchy problem may be solvable only if  . In that case, if
. In that case, if 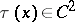 ,
,  , a solution indeed exists and is given by
, a solution indeed exists and is given by
 |
where  is any function of class
is any function of class  ,
, 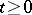 , satisfying the conditions
, satisfying the conditions  .
.
A necessary condition for the existence of a solution to a characteristic Cauchy problem for a linear system of hyperbolic equations is that the rank of the augmented matrix of the system equals the rank of the singular matrix along the characteristic surface 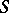 .
.
There is a wide class of hyperbolic equations and systems for which one may take a characteristic surface as an initial surface. For example, for the equation
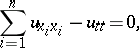 | (1) |
when the characteristic surface 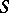 is the cone
is the cone
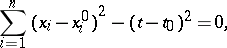 | (2) |
the characteristic Cauchy problem may be phrased as follows: Find a solution  of equation (1) which is regular within the cone (2) and takes prescribed values on the cone (2).
of equation (1) which is regular within the cone (2) and takes prescribed values on the cone (2).
In the case of a space-like variable (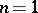 ,
,  ), the cone (2) is a pair of straight lines
), the cone (2) is a pair of straight lines 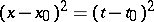 passing through the point
passing through the point 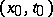 . These straight lines divide the plane
. These straight lines divide the plane  of the variables
of the variables 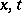 into four angles. Let the domain
into four angles. Let the domain  be one of these angles. Then the characteristic problem is customarily known as the Goursat problem: Determine a solution
be one of these angles. Then the characteristic problem is customarily known as the Goursat problem: Determine a solution 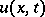 of the equation
of the equation
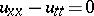 |
which is regular in  and satisfies the conditions
and satisfies the conditions
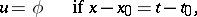 |
 |
 |
If the characteristic surface 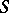 is at the same time a surface of degenerate type or order, the characteristic Cauchy problem may prove to be well-posed.
is at the same time a surface of degenerate type or order, the characteristic Cauchy problem may prove to be well-posed.
For the equation
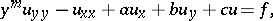 | (3) |
which is hyperbolic for 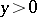 , the curve of degeneracy
, the curve of degeneracy 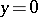 is a characteristic. If
is a characteristic. If  , the Cauchy problem
, the Cauchy problem
 | (4) |
for equation (3) is well-posed, but if  it becomes ill-posed. In that case it is natural to investigate the problem either with modified initial data:
it becomes ill-posed. In that case it is natural to investigate the problem either with modified initial data:
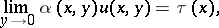 |
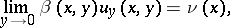 |
 |
or with incomplete initial data, i.e. dropping one of the conditions (4).
References
| [1] | V.S. Vladimirov, "Equations of mathematical physics" , MIR (1984) (Translated from Russian) |
| [2] | S.K. Godunov, "The equations of mathematical physics" , Moscow (1971) (In Russian) |
| [3] | F.G. Tricomi, "Equazioni a derivate parziale" , Cremonese (1957) |
| [4] | L. Bers, F. John, M. Schechter, "Partial differential equations" , Interscience (1964) |
| [5] | A.V. Bitsadze, D.F. Kalinichenko, "A collection of problems on the equations of mathematical physics" , Moscow (1977) (In Russian) |
| [6] | A.V. Bitsadze, "Linear partial differential equations of mixed type" , Proc. 3-rd All-Union Math. Congress , 3 , Moscow (1958) (In Russian) |
Comments
The more common English term for this problem is characteristic Cauchy problem. A general discussion is given in [a1], Sect. 12.8.
References
| [a1] | L.V. Hörmander, "The analysis of linear partial differential operators" , 2 , Springer (1983) |
| [a2] | A.V. Bitsadse, "Equations of mixed type" , Pergamon (1964) (Translated from Russian) |
| [a3] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German) |
Cauchy characteristic problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cauchy_characteristic_problem&oldid=13736