Cauchy-Hadamard theorem
Consider a complex power series
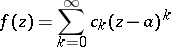 | (1) |
and let
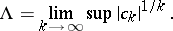 |
If 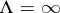 , then the series (1) is convergent only at the point
, then the series (1) is convergent only at the point  ; if
; if 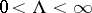 , then the series (1) is absolutely convergent in the disc
, then the series (1) is absolutely convergent in the disc 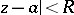 where
where
 | (2) |
and divergent outside the disc, where 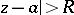 ; if
; if 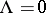 , the series (1) is absolutely convergent for all
, the series (1) is absolutely convergent for all 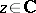 . The content of the Cauchy–Hadamard theorem is thus expressed by the Cauchy–Hadamard formula (2), which should be understood in this context in a broad sense, including
. The content of the Cauchy–Hadamard theorem is thus expressed by the Cauchy–Hadamard formula (2), which should be understood in this context in a broad sense, including 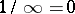 and
and 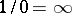 . In other words, the Cauchy–Hadamard theorem states that the interior of the set of points at which the series (1) is (absolutely) convergent is the disc
. In other words, the Cauchy–Hadamard theorem states that the interior of the set of points at which the series (1) is (absolutely) convergent is the disc 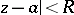 of radius (2). In the case of a real power series (1), formula (2) defines the "radius" of the interval of convergence:
of radius (2). In the case of a real power series (1), formula (2) defines the "radius" of the interval of convergence: 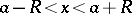 . Essentially, the Cauchy–Hadamard theorem was stated by A.L. Cauchy in his lectures [1] in 1821; it was J. Hadamard [2] who made the formulation and the proof fully explicit.
. Essentially, the Cauchy–Hadamard theorem was stated by A.L. Cauchy in his lectures [1] in 1821; it was J. Hadamard [2] who made the formulation and the proof fully explicit.
For power series
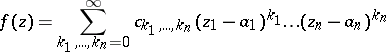 | (3) |
in  complex variables
complex variables  ,
, 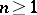 , one has the following generalization of the Cauchy–Hadamard formula:
, one has the following generalization of the Cauchy–Hadamard formula:
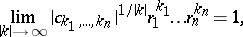 | (4) |
 |
which is valid for the associated radii of convergence  of the series (3) (see Disc of convergence). Writing (4) in the form
of the series (3) (see Disc of convergence). Writing (4) in the form  , one obtains an equation defining the boundary of a certain logarithmically convex Reinhardt domain with centre
, one obtains an equation defining the boundary of a certain logarithmically convex Reinhardt domain with centre  , which is the interior of the set of points at which the series (3) is absolutely convergent (
, which is the interior of the set of points at which the series (3) is absolutely convergent ( ).
).
References
| [1] | A.L. Cauchy, "Analyse algébrique" , Gauthier-Villars , Leipzig (1894) (German translation: Springer, 1885) |
| [2] | J. Hadamard, "Essai sur l'etude des fonctions données par leur développement de Taylor" J. Math. Pures Appl. , 8 : 4 (1892) pp. 101–186 (Thesis) |
| [3] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
| [4] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) |
Comments
The Cauchy–Hadamard theorem is related to Abel's lemma: Let in (3)  and suppose that for some constant
and suppose that for some constant  , some
, some 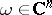 and for all
and for all 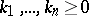 :
:
 |
Then the power series in (3) converges absolutely in the polydisc 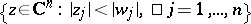 (see [a1], Sect. 2.4). This fact makes power series an effective tool in the analytic continuation of analytic functions of several variables (see also Hartogs theorem).
(see [a1], Sect. 2.4). This fact makes power series an effective tool in the analytic continuation of analytic functions of several variables (see also Hartogs theorem).
References
| [a1] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) pp. Chapt. 2.4 |
Cauchy-Hadamard theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cauchy-Hadamard_theorem&oldid=13956