Category of a set

A topological characterization of the "massiveness" of a set. A subset 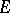of a topological space 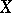is said to be of the first category in 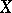if it can be expressed as a finite or countable union of nowhere-dense sets in 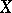. Otherwise 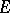is said to be of the second category. Sometimes the complement in 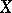of a set of the first category is also called a set of the second category. In modern literature (see [2]) such sets (in the case of a Baire space) are called residual or comeager. A non-empty closed set of real numbers, in particular an interval, is not of the first category in itself [1]. This result generalizes to any complete metric space. This generalization has wide application in analysis. The role of a set of the first category in analysis is analogous to that of a null set in measure theory. However, a set of the first category can be a set of full measure, while there are null sets of the second category.

References

[1]	R. Baire, "Leçons sur les fonctions discontinues, professées au collège de France" , Gauthier-Villars (1905)
[2]	J.C. Oxtoby, "Measure and category" , Springer (1971)

Comments

A set of the first category is also called a meager set. The statement that a complete metric space is not of the first category in itself is known as Baire's category theorem (cf. [a1]).

Examples of sets that are meager and not null, as well as of those that are null and not meager, can be found in [a2], Th. 5.5.

References

[a1]	H.L. Royden, "Real analysis" , Macmillan (1968)
[a2]	A.C.M. van Rooy, W.H. Schikhof, "A second course on real functions" , Cambridge Univ. Press (1982)