Category cohomology
Let $\mathcal{C}$ be a small category, $\mathcal{A}$ an Abelian category with exact infinite products, and $M : \mathcal{C} \rightarrow \mathcal{A}$ a covariant functor. Define the objects $C ^ { n } ( \mathcal{C} , M )$ for $n \geq 0$ in the following way:
\begin{equation*} C ^ { 0 } ( \mathcal{C} , M ) = \prod _ { C \in \text{OC} } M ( C ), \end{equation*}
\begin{equation*} C ^ { n } ( {\cal C} , M ) = \prod _ { \langle \alpha _ { 1 } , \dots , \alpha _ { n } \rangle } M ( \operatorname { codom } \alpha _ { n } ) , n > 0, \end{equation*}
where $( \alpha _ { 1 } , \dots , \alpha _ { n } )$ is a sequence of morphisms of $\mathcal{C}$ with $\operatorname { codom} \alpha _ { i } = \operatorname { dom } \alpha _ { i + 1 }$, $1 \leq i \leq n - 1$. Let
\begin{equation*} d ^ { n } : C ^ { n } ( \mathcal{C} , M ) \rightarrow C ^ { n + 1 } ( \mathcal{C} , M ) \end{equation*}
be the monomorphism induced by the family of morphisms
\begin{equation*} \{ M ( \alpha ) \text { pr} _ { \text {dom } \alpha } - \text { pr}_{ \text {codom } \alpha } \}_{ \alpha} \quad \text { for } n = 0, \end{equation*}
and by the family
\begin{equation*} \{ M ( \alpha _ { n +1} ) \text { pr }_{ ( \alpha _ { 1 } , \dots , \alpha _ { n } )}+ \end{equation*}
\begin{equation*} +\sum _ { i < n + 1 } ( - 1 ) ^ { n + 1 - i } \operatorname { pr }_{ ( \alpha _ { 1 } , \dots , \alpha _ { i + 1 } \alpha _ { i } , \ldots , \alpha _ { n + 1 } ) }+ \end{equation*}
\begin{equation*} \left. + ( - 1 ) ^ { n + 1 } \operatorname { pr }_{ ( \alpha _ { 2 } , \dots , \alpha _ { n + 1 } ) }\right\}_{ ( \alpha _ { 1 } , \dots , \alpha _ { n + 1 } )} \end{equation*}
\begin{equation*} \text{for} \, n > 0. \end{equation*}
Here, $\operatorname { pr } _{( \alpha _ { 1 } , \dots , \alpha _ { n } )}$ denotes the projection $C ^ { n } ( \mathcal{C} , M ) \rightarrow M( \operatorname{ codom } \alpha_n$).
The morphisms $d ^ { n }$, $n \geq 0$ satisfy the conditions $d ^ { n + 1 } d ^ { n } = 0$, and therefore one obtains a complex $C ^ { * } ( \mathcal{C} , M )$ in $\mathcal{A}$. The homology objects of this complex are called the cohomology of $\mathcal{C}$ with coefficients in $M$ and are denoted by $H ^ { n } ( \mathcal{C} , M )$. For any functor $M : \mathcal{C} \rightarrow \mathcal{A}$ there are a functor $c M : \mathcal{C} \rightarrow A$ (called the co-induced functor) and a monomorphism $M \rightarrow c M$ such that $H ^ { n } ( \mathcal{C} , cM ) = 0$ for $n > 0$.
The functor $C ^ { * } ( \mathcal{C} , - )$ is an exact functor. Therefore, any short exact sequence of functors induces a long exact sequence of cohomology objects of $\mathcal{C}$. It can be proved that the functors $\{ H ^ { n } ( \mathcal{C} , - ) : n \geq 0 \}$ form a universal connected (exact) sequence of functors and that
\begin{equation*} H ^ { n } ( {\cal C} , M ) = \underline{\operatorname { lim }} \leftarrow ^ { n } M, \end{equation*}
where $\underline{\operatorname { lim }} \leftarrow ^ { n }$ is $n$th right satellite of the functor $\operatorname { \underline{lim} } \leftarrow : \mathcal{A} ^ { \mathbf{C} } \rightarrow A$ (here, $\mathcal{A } ^ { \text{C} }$ denotes the category of functors from $\mathcal{C}$ to $\mathcal{A}$, and $\underline{\operatorname{lim}} \leftarrow$ is an (inverse) limit functor).
For a small category $\mathcal{C}$, let $Z \mathcal C $ denote the pre-additive category whose objects are those of $\mathcal{C}$ and $Z \mathcal{C} ( C , C^{\prime} )$ is the free Abelian group on $\mathcal{C} ( C , C ^ { \prime } )$ (cf. also Free group). Composition is defined in the unique way so as to be bilinear and to make the inclusion ${\cal C} \rightarrow {\bf Z} {\cal C}$ a functor. If $\mathcal{C}$ is a monoid, then $Z \mathcal C $ is the monoid ring of $\mathcal{C}$ with coefficients in $Z$. The inclusion ${\cal C} \rightarrow {\bf Z} {\cal C}$ induces an isomorphism of categories
\begin{equation*} \text{Ab} ^ { \text{ZC} } \approx \text{Ab} ^ { \text{C} } \end{equation*}
where the left-side is the category of additive functors from $Z \mathcal C $ to $\operatorname{Ab}$ (the category of Abelian groups) and the right-hand side side is the category of all functors from $\mathcal{C}$ to $\operatorname{Ab}$.
If $\mathcal{A}$ is the category of Abelian groups (${\cal A} = \operatorname{Ab}$), one has
\begin{equation*} H ^ { n } ( {\cal C} , M ) = \operatorname { Ext } _ { Z {\bf C} } ^ { n } ( {\cal Z} , M ), \end{equation*}
where $\mathcal Z$ denotes the constant functor $Z \mathcal{C} \rightarrow \operatorname{Ab}$ (i.e. $Z ( C ) = \mathcal{Z}$, $Z ( \alpha ) = 1 _ { \mathbf{Z} }$ for any object $C$ and any morphism $\alpha$ of $\mathcal{C}$), and 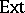 is taken in the category of additive functors $\text{Ab} ^ { \text{ZC} }$.
is taken in the category of additive functors $\text{Ab} ^ { \text{ZC} }$.
If $\mathcal{C}$ is a group (i.e. a category with one object and whose morphisms are invertible) and ${\cal A} = \operatorname{Ab}$, then the groups $H ^ { n } ( \mathcal{C} , M )$ are the cohomology groups (cf. also Cohomology group) of the group $\mathcal{C}$ with coefficients in $M$, which is a module over the group ring $Z \mathcal C $ (cf. also Cross product). In this case the co-induced functor $c M$ is a co-induced $Z \mathcal C $-module $\operatorname{Ab} ( Z ({\cal C} ) , M )$.
As for the case of groups, $n$-fold extensions of categories can be defined and the isomorphism with $n + 1$ cohomologies of categories can be established. Under additional assumptions, the properties of group cohomologies are obtained for category cohomologies (e.g. the universal coefficient formula for the cohomology group of a category, etc.).
For a commutative ring $K$, a $K$-category is a category $\mathcal{C}$ equipped with a $K$-module structure on each hom-set in such a way that composition induces a $K$-module homomorphism. If $K = \mathcal{Z}$, a $\mathcal Z$-category is just a pre-additive category. B. Mitchell has defined the (Hochshild) cohomology group of a small $K$-category $\mathcal{C}$ with coefficients in a bimodule (i.e., bifunctor) $F : {\cal C} ^ { * } \otimes _ { k } {\cal C} \rightarrow \operatorname{Ab}$ (where $\mathcal{C} ^ { * } \otimes_{ k} \mathcal{C}$ denotes the tensor product of categories). H.-J. Baues and G. Wirshing have introduced cohomology of a small category with coefficients in a natural system, which generalizes known concepts and uses Abelian-group-valued functors (i.e. modules) and bifunctors as coefficients.
References
| [a1] | H.-J. Baues, G. Wirshing, "Cohomology of small categories" J. Pure Appl. Algebra , 38 (1985) pp. 187–211 |
| [a2] | T. Datuashvili, "The cohomology of categories" Tr. Tbiliss. Mat. Inst. A. Razmadze, Akad. Nauk Gruzin.SSR , 62 (1979) pp. 28–37 |
| [a3] | G. Hoff, "On the cohomology of categories" Rend. Math. (VI) , 7 : 2 (1974) pp. 169–192 |
| [a4] | M.J. Lee, "A generalized Mayer–Vietoris sequence" Math. Jap. , 19 : 1 (1974) pp. 41–50 |
| [a5] | B. Mitchell, "Rings with several objects" Adv. Math. , 8 (1972) pp. 1–161 |
| [a6] | D.G. Quillen, "Higher algebraic $K$-theories" H. Bass (ed.) , Algebraic $K$-theory I , Lecture Notes Math. , 341 , Springer (1973) pp. 85–147 |
| [a7] | J.-E. Roos, "Sur les foncteurs derives de $\operatorname { lim }_\lambda$. Applications" C.R. Acad. Sci. Paris , 252 (1961) pp. 3702–3704 |
| [a8] | Ch.E. Watts, "A homology theory for small categories" , Proc. Conf. Categorical Algebra (La Jolla, Calif., 1965) , Springer (1966) pp. 331–335 |
Category cohomology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Category_cohomology&oldid=55405